OxyPlot 라이브러리로 복소수 표현
요즘 "코딩 더 매트릭스" 책을 읽고 있습니다.
코딩 더 매트릭스
; http://www.yes24.co.kr/24/goods/17967245
Coding the Matrix Resources
; http://resources.codingthematrix.com/
내부 코드가 파이썬으로 되어 있는데, 역시 쉽군요. ^^ 그래도 C#으로 실습해 보는 것도 재미있겠다 싶습니다.
가령, 2장 4절에 보면 "복소수 필드 C 다루기"가 나오는데요.
복소수의 경우 .NET 4.0부터 추가된 System.Numerics 어셈블리가 있어 별다른 어려움없이 사용할 수 있습니다. 게다가 자바와는 달리 연산자 재정의가 가능하므로 (파이썬만큼 편하지는 않지만) 직관적인 사칙 연산 표현도 가능합니다.
using System;
using System.Numerics;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
Complex n1 = new Complex(1, 3);
Complex n2 = new Complex(10, 20);
Console.WriteLine(n1 + n2); // 출력: (11, 23)
Console.WriteLine(n1.Real);
Console.WriteLine(n1.Imaginary);
}
}
}
복소수를 복소 평면에 시각화하는 도구로는 OxyPlot같은 라이브러리를 쓰면 됩니다.
C# Plotting 라이브러리 OxyPlot
; https://www.sysnet.pe.kr/2/0/10973
책에서 (별도 파일로 제공되는) plot 모듈은 복소수를 받아 내부적으로 SVG 파일로 변환을 하는데요. OxyPlot은 정해진 타입이 있으므로 그것으로 변환을 해주면 됩니다. 대충 다음과 같은 도우미 클래스를 하나 두고,
static class Helper
{
public static void Add(this ScatterSeries scatter, Complex item)
{
scatter.Add(item.Real, item.Imaginary);
}
public static void Add(this ScatterSeries scatter, double real, double imagine)
{
scatter.Points.Add(new ScatterPoint(real, imagine));
}
public static void Add(this ScatterSeries scatter, IEnumerable<Complex> points)
{
if (points == null)
{
return;
}
foreach (Complex item in points)
{
scatter.Add(item);
}
}
}
이렇게 사용해 주면 됩니다.
protected override void OnLoad(EventArgs e)
{
// ...[생략]...
Complex[] S = new Complex[]
{
new Complex(2, 2),
new Complex(3, 2),
new Complex(1.75, 1),
new Complex(2, 1),
new Complex(2.25, 1),
new Complex(2.5, 1),
new Complex(2.75, 1),
new Complex(3, 1),
new Complex(3.25, 1),
};
ScatterSeries series = PlotsFromComplex(tS);
_pm.Series.Add(series);
// ...[생략]...
}
private ScatterSeries PlotsFromComplex(IEnumerable<Complex> complex)
{
ScatterSeries series = new ScatterSeries();
series.MarkerType = MarkerType.Circle;
series.Add(complex);
return series;
}
그럼, 책에서 나온 것과 같은 출력 화면을 볼 수 있습니다.
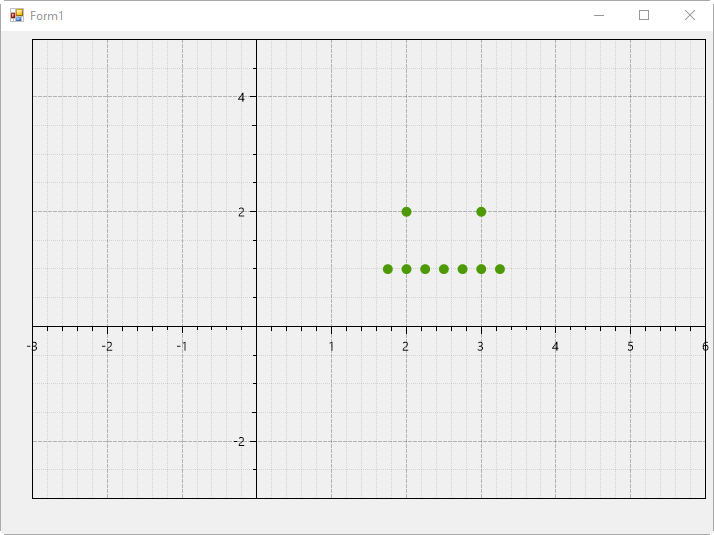
복소수 덧셈으로 인한 평행 이동은 LINQ로 간단하게 표현이 가능합니다. 예를 들어, 위의 이미지에 출력된 S 목록에 (1, 2i) 만큼의 평행이동(translation)을 한다면 다음의 코드로 끝입니다.
Complex[] S = new Complex[]
{
// ...[생략]...
};
Complex z = new Complex(1, 2);
var tS = from item in S
select item + z;
물론, 스케일링(scaling)도 가능하고.
var tS = from item in S
select item * (1.0 / 2); // 복소수의 실수/허수 좌표를 반으로 줄임
-1로 곱하면 180도 회전도 되고,
var tS = from item in S
select item * -1;
i를 곱하면 90도 회전도 됩니다.
Complex z = new Complex(0, 1);
var tS = from item in S
select item * z;
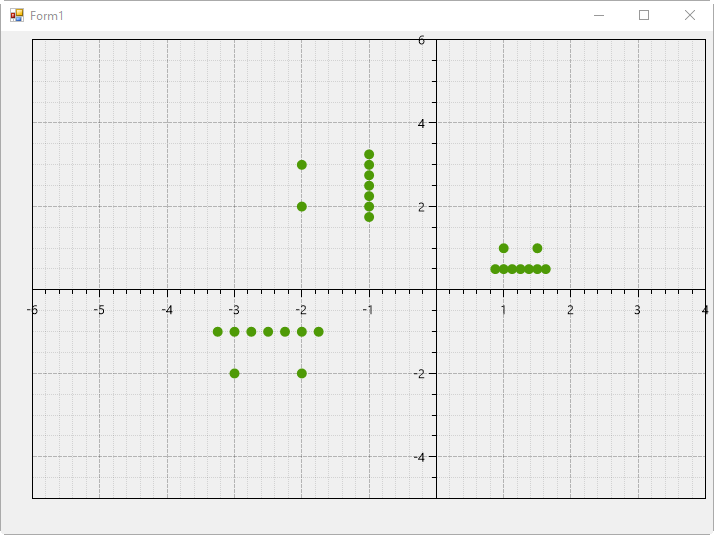
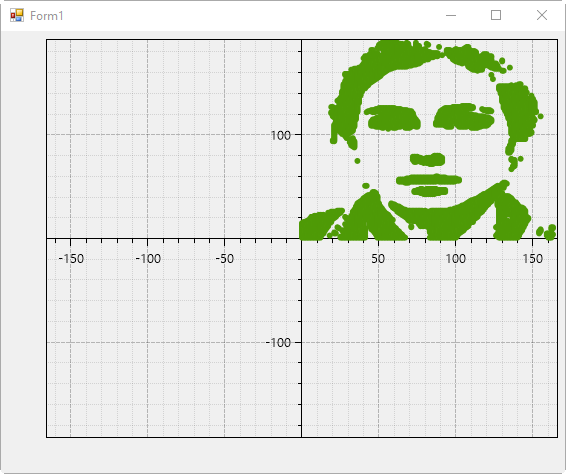
이미지 데이터를 복소수화하는 것은 약간의 코드를 곁들이면 OK! ^^
var images = FromImage("img01.png");
private IEnumerable<Complex> FromImage(string filePath)
{
List<Complex> list = new List<Complex>();
using (Bitmap bitmap = Image.FromFile(filePath) as Bitmap)
{
for (int x = 0; x < bitmap.Width; x++)
{
for (int y = 0; y < bitmap.Height; y++)
{
Color color = bitmap.GetPixel(x, y);
if (color.GetBrightness() < 0.5)
{
Complex z = new Complex(x, -y + bitmap.Height);
list.Add(z);
}
}
}
}
return list;
}
(
첨부 파일은 이 글의 예제 코드를 포함합니다.)
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]