C# - 오일러 공식을 이용한 복소수 값의 라디안 회전
역시 "코딩 더 매트릭스"의 이야기입니다.
코딩 더 매트릭스
; http://www.yes24.co.kr/24/goods/17967245
복소수 z를 오일러 공식에 따라 τ 만큼 회전한 것을 나타내는 함수가 이렇다는 군요. ^^
f(z) = z * eτi
복소수 승수 값을 닷넷 BCL의 Math.Pow가 제공하지 않으므로 다음의 글에 설명된 Power 메서드를 사용하시면 됩니다.
C# - 복소수 타입의 승수를 지원하는 Power 메서드
; https://www.sysnet.pe.kr/2/0/10975
따라서, 이를 이용하면 복소수의 회전 메서드를 다음과 같이 구현할 수 있습니다.
public static readonly Complex i = new Complex(0, 1);
public static readonly Complex e = new Complex(Math.E, 0);
public static Complex Rotate(this Complex src, double radian)
{
return src * e.Power(i * radian);
}
회전 메서드가 만들어졌으니, 이제 복소수 컬렉션에 대한 회전 처리는 LINQ의 도움을 받아 쉽게 처리할 수 있습니다.
Complex[] S = new Complex[]
{
new Complex(2, 2),
new Complex(3, 2),
new Complex(1.75, 1),
new Complex(2, 1),
new Complex(2.25, 1),
new Complex(2.5, 1),
new Complex(2.75, 1),
new Complex(3, 1),
new Complex(3.25, 1),
};
var tS1 = from item in S
select item.Rotate(Math.PI / 4);
var tS2 = from item in S
select item.Rotate(Math.PI / 2);
var tS3 = from item in S
select item.Rotate(Math.PI);
이를 OxyPlot 라이브러리로 표현하면,
OxyPlot 라이브러리로 복소수 표현
; https://www.sysnet.pe.kr/2/0/10974
이렇게 나옵니다. ^^
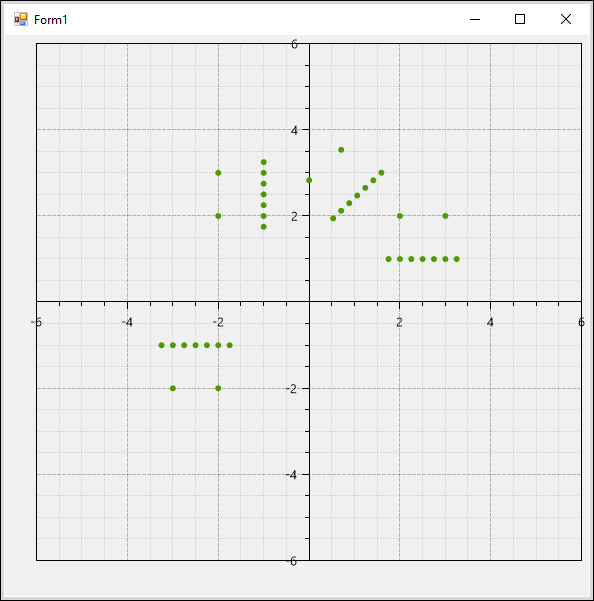
(
첨부 파일은 이 글의 예제 코드를 포함합니다.)
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]