Euler's totient function - C#
*** 유의사항: "프로젝트 오일러의 70번 문제"를 풀지 않은 분들의 경우 가능한 문제를 풀고 나서 읽기를 바랍니다.
"프로젝트 오일러" 문제의 69번과 70번 문제는 오일러의 φ(Phi) 함수를 구하는 수학적 지식이 있어야 합니다. 이번 글은 제가 그 문제를 푸는 과정에서 헤맸던 사항을 정리한 것에 불과하고, 제 지식의 한계로 ^^; 그 어떤 증명이나 수학적인 과정들을 포함하고 있지는 않습니다.
일단, 저는 φ(Phi) 함수를 모른 상태에서 10의 7승을 가볍게 생각하고 덤벼들었습니다. 즉, 다음과 같이 각각의 수마다 공약수가 있는지를 기반으로 계산을 시작했더랬습니다.
for (int i = 2; i < 1000000; i ++)
{
int relativelyPrimeCount = 0;
for (int j = 1; j < i; j ++)
{
if (유클리드호제법(i, j) == true)
{
relativelyPrimeCount ++;
}
}
...[생략]...
}
이 방법이 아닐 거라는 것을 아는 데에는 그리 오래 걸리진 않았습니다. ^^; (원래, "프로젝트 오일러"의 모든 문제는 1분 내에 계산이 나오도록 출제되었다고 합니다.)
따라서, 뭔가 수학적인 계산이 필요함을 알게 되었고 검색을 해서 오일러의 파이 함수를 구하는 공식을 찾아냈습니다.
Euler's totient function
; http://en.wikipedia.org/wiki/Totient#Euler.27s_product_formula
위의 그림에 보면 범용적으로 다음과 같은 계산을 통해서 구할 수 있다고 나옵니다. (역시, 수학자들은 머리가 비상합니다. ^^ 어쩜 저렇게 표기도 멋있게 하는지!)
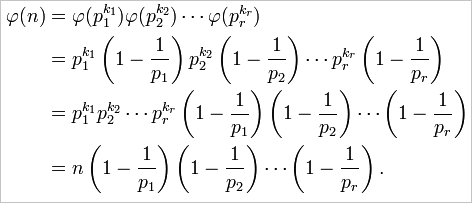
위와 같이 씌여지면 '비(非) 수학자'들은 당황할 수 있는데 ^^ 그 아래에 있는 예제 식을 보면 금방 이해가 됩니다.
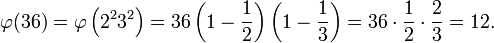
숫자 36은 소인수 분해를 하면 2, 3 값이 나옵니다. 따라서, 파이 함수 값은 36 * (1 - 1/2)(1 - 1/3) = 12라는 계산을 통해서 구할 수 있는 것입니다. 이 때문에 ^^ 지난번에 소인수 분해를 하는 함수를 다룬 이야기를 쓴 것입니다.
소수 판정 및 소인수 분해 소스 코드 - C#
; https://www.sysnet.pe.kr/2/0/1255
이렇게 해서 파이 함수를 C#으로 작성하면 대강 다음과 같이 나옵니다.
static int GetPhiCount(int targetNumber)
{
// 소인수를 모두 구하고,
List<int> primes = new List<int>();
int tempNumber = targetNumber;
for (int i = 2; i * i <= tempNumber;)
{
if (tempNumber % i == 0)
{
primes.Add(i);
tempNumber = tempNumber / i;
}
else
{
i++;
}
}
primes.Add(tempNumber);
double product = 1;
// Euler's totient function 계산을 합니다.
for (int i = 0; i < primes.Count; i++)
{
product = product * (1 - (double)1 / primes[i]);
}
return (int)(product * targetNumber);
}
위와 같이 계산하고 실행하면, 다음과 같이 계산이 되어 답이 9708131로 나옵니다.
[0]21 ==> 1.75 (21, 12)
[1]291 ==> 1.515625 (291, 192)
[2]2817 ==> 1.50480769230769 (2817, 1872)
[3]2991 ==> 1.50150602409639 (2991, 1992)
[4]4435 ==> 1.25141083521445 (4435, 3544)
[5]20617 ==> 1.02185765265662 (20617, 20176)
[6]23729 ==> 1.01933072726492 (23729, 23279)
[7]49781 ==> 1.01654040146209 (49781, 48971)
[8]75841 ==> 1.00873856139604 (75841, 75184)
[9]118577 ==> 1.00595546129374 (118577, 117875)
[10]176569 ==> 1.00496880976232 (176569, 175696)
[11]209681 ==> 1.00474385574845 (209681, 208691)
[12]223121 ==> 1.00445682952852 (223121, 222131)
[13]284029 ==> 1.00384887255248 (284029, 282940)
[14]400399 ==> 1.00340567361668 (400399, 399040)
[15]474883 ==> 1.00294622038996 (474883, 473488)
[16]704129 ==> 1.00243444439857 (704129, 702419)
[17]732031 ==> 1.00235378851778 (732031, 730312)
[18]778669 ==> 1.00228215874454 (778669, 776896)
[19]783169 ==> 1.0022690159663 (783169, 781396)
[20]979571 ==> 1.00202538689493 (979571, 977591)
[21]989537 ==> 1.0020232112352 (989537, 987539)
[22]1288663 ==> 1.00178409288788 (1288663, 1286368)
[23]1405913 ==> 1.00170571256962 (1405913, 1403519)
[24]1504051 ==> 1.00169629917736 (1504051, 1501504)
[25]1514419 ==> 1.00163696539025 (1514419, 1511944)
[26]1617953 ==> 1.00159343411051 (1617953, 1615379)
[27]1679567 ==> 1.00154564021527 (1679567, 1676975)
[28]1945241 ==> 1.00143632966803 (1945241, 1942451)
[29]2094901 ==> 1.00143266612617 (2094901, 2091904)
[30]2239261 ==> 1.0013724224038 (2239261, 2236192)
[31]2710627 ==> 1.00125996595765 (2710627, 2707216)
[32]2868469 ==> 1.00124716569118 (2868469, 2864896)
[33]3159587 ==> 1.00117494999016 (3159587, 3155879)
[34]3582907 ==> 1.00111402322488 (3582907, 3578920)
[35]3689251 ==> 1.0011014351491 (3689251, 3685192)
[36]4079147 ==> 1.00108670070255 (4079147, 4074719)
[37]4696009 ==> 1.00107632552825 (4696009, 4690960)
[38]5050429 ==> 1.00089359323969 (5050429, 5045920)
[39]5380657 ==> 1.0008923223447 (5380657, 5375860)
[40]5459471 ==> 1.00085796137744 (5459471, 5454791)
[41]5886817 ==> 1.00084003811029 (5886817, 5881876)
[42]6018163 ==> 1.00083067694101 (6018163, 6013168)
[43]6159431 ==> 1.00081892749421 (6159431, 6154391)
[44]6606071 ==> 1.00081809864482 (6606071, 6600671)
[45]6636841 ==> 1.00077763053849 (6636841, 6631684)
[46]7188239 ==> 1.00075179187505 (7188239, 7182839)
[47]7357291 ==> 1.00074798090044 (7357291, 7351792)
[48]7507321 ==> 1.00074502794821 (7507321, 7501732)
[49]7983917 ==> 1.0007242290464 (7983917, 7978139)
[50]8219537 ==> 1.00069906784866 (8219537, 8213795)
[51]8849513 ==> 1.00067778448828 (8849513, 8843519)
[52]9708131 ==> 1.00064936196064 (9708131, 9701831)
그런데, 이 답은 옳지 않다고 판정되었습니다. 제가 이 단계에서 ^^; 거의 이틀을 고민했습니다. 혹시 파이 함수를 구하는 내부 코드에 문제가 있는 것은 아닌지...? 내가 모르는 뭔가 특별한 수학적 지식이 포함되어야 하는 것은 아닌지...? 와 같은 별의별 가정을 다 해보았는데, 결국 문제를 쉽게 식별하지 못했던 가장 큰 이유는,,, 코드를 쳐다보는 눈이 '리턴값'을 주목하는 데 오래 걸렸기 때문이었습니다.
설마... 리턴값이 잘못 되었으리라고는 상상도 못했는데요.
다시 "Euler's totient function" 공식을 보시면, 분수를 포함하므로 결국 값들이 double 형으로 계산이 되는 것을 알 수 있습니다. 따라서 단순히 (int) 값으로 형변환하면 값이 절삭이 되어 결과가 틀어져 버리는 것입니다. 위의 계산값들을 보면 미세한 n / φ(n) 결과값이 0.0001로 순위가 차이가 나기 때문에 (int) 형변환으로 인한 오차는 클 수밖에 없었던 것이지요.
(int) 절삭의 효과는 테스트 해보면 다음과 같습니다.
Console.WriteLine(((int)1.3));
Console.WriteLine(((int)1.6));
1
1
Console.WriteLine(((int)Math.Round(1.3)));
Console.WriteLine(((int)Math.Round(1.6)));
1
2
따라서, 반환값을 (int) 형변환하기 전에, Math.Round로 보정을 해주면 "프로젝트 오일러" 측에서 원하는 답이 나옵니다. ^^; 일단 그걸로 답을 내었으니 급한 불은 껐고. 이제 성능 개선을 해볼 차례입니다.
그래서, 조금 더 들여다 보면 파이 함수의 재미있는 성질을 발견하게 됩니다.
오일러 피 함수
; http://ko.wikipedia.org/wiki/%EC%98%A4%EC%9D%BC%EB%9F%AC_%ED%94%BC_%ED%95%A8%EC%88%98
위의 글에 보면 다음과 같은 공식이 나옵니다.
p가 소수일 때, φ(p) = p - 1
예를 들어, p == 13이면, (소수의 성질이라 당연하겠지만) 12를 반환하면 되는 것입니다. 만약 이 값을 기존 "Euler's totient function"에 대입하면 다음과 같이 소수점이 포함된 값이 나옵니다.
φ(13) = 13 * (1 - 1/13)
= 13 * 0.92307692307692313 (923076이 반복되는 무한 소수)
물론, 거의 12가 나오긴 하지만 엄밀히 (13 - 1) != 13 * 0.92307692307692313이므로 정확하게 반환해주는 공식을 추가하는 것이 좋겠습니다.
이렇게 소수들에 대한 파이 함수 값을 구하고 나면 다시 한번 재미있는 성질을 찾을 수 있는데요.
m, n이 서로소인 정수일 때, φ(mn) = φ(m)φ(n)
위의 2가지 성질로 인해서 정수값으로 반환할 수 있는 좀 더 많은 기회가 생깁니다. 왜냐하면, 모든 수는 소수 아니면, 소인수 분해되어 결국 소수의 곱으로 바뀌기 때문에 중간에 나오는 소수의 정수값을 보관해 두었다가 다른 수의 소인수 분해에 그 값의 곱을 이용하면 되기 때문입니다.
그런데, 위의 경우로 걸러지지 않는 수들이 있습니다. 바로 4와 같은 수인데, 이런 경우 φ(2 * 2) != φ(2)φ(2)입니다. 즉, m과 n이 서로소라는 조건에 맞지 않으므로 계산이 틀려지는데요. 그런데, 다음과 같은 성질도 있어서 4는 여기에 대입해 줄 수 있습니다.
φ(pk) = pk - p(k - 1) = pk - 1 * (p - 1)
그래서, 함수는 최종적으로 다음과 같이 바뀔 수 있습니다.
static List<int> _primes = new List<int>();
static int GetPhiCount2(Dictionary<int, int> primePhi, int targetNumber)
{
// 소인수를 모두 구하고
Dictionary<int, int> primes = new Dictionary<int, int>();
int tempNumber = targetNumber;
int primeCount = 0;
int firstPrimeNumber = 0;
int secondPrimeNumber = 0;
for (int n = 0; n < _primes.Count; )
{
int prime = _primes[n];
if (prime * prime > targetNumber)
{
break;
}
if (tempNumber % prime == 0)
{
if (primes.ContainsKey(prime) == true)
{
primes[prime]++;
}
else
{
primes.Add(prime, 1);
}
primeCount++;
firstPrimeNumber = prime;
tempNumber = tempNumber / prime;
}
else
{
n++;
}
}
if (primes.Count == 0)
{
// 적용 1: p가 소수일 때, φ(p) = p - 1
_primes.Add(targetNumber);
primePhi.Add(targetNumber, targetNumber - 1);
return targetNumber - 1;
}
if (tempNumber != 1)
{
primes.Add(tempNumber, 1);
secondPrimeNumber = tempNumber;
primeCount++;
}
if (primes.Count == 2 && primeCount == 2)
{
// 적용 2: m,n이 서로소인 정수일 때, φ(mn) = φ(m)φ(n)
return primePhi[firstPrimeNumber] * primePhi[secondPrimeNumber];
}
else if (primes.Count == 1)
{
// 적용 3: φ(pk) = pk - p(k - 1) = pk - 1 * (p - 1)
int k = primes[firstPrimeNumber];
return PowOf(firstPrimeNumber, k - 1) * (firstPrimeNumber - 1);
}
double product = 1;
foreach (var aPrimeKey in primes.Keys)
{
product = product * (1 - (double)1 / aPrimeKey);
}
return (int)Math.Round(product * targetNumber);
}
static int PowOf(int p, int k)
{
int result = 1;
while (k-- > 0)
{
result = result * p;
}
return result;
}
함수는 길어졌지만, 탈출구가 많아졌기 때문에 이렇게 계산하면 결과를 20초 안에 끊을 수 있습니다. 위의 방법은 지난번
"소인수 분해"의 마지막 부분에서 소수를 재활용하는 방법까지 사용된 것입니다.
첨부된 파일은 위의 코드를 포함한 예제 프로젝트입니다.
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]