Unity로 실습하는 Shader (10) - 빌보드 구현
지난번에 만든 shader에 이어서 살펴보겠습니다.
Unity로 실습하는 Shader (9) - 투명 배경이 있는 텍스처 입히기
; https://www.sysnet.pe.kr/2/0/11631
위의 작업에 따라 Unity 세계에 배치한 나무 한 그루가 있을 때 카메라를 움직여 나무가 위치한 곳의 옆으로 이동해 보겠습니다. 이를 위해 Unity에서 화살표 키를 이용해 카메라를 움직일 수 있도록 다음과 같은 작업을 해둡니다.
C# - Unity에서 캐릭터가 바라보는 방향을 기준으로 카메라의 위치 이동 및 회전하는 방법
; https://www.sysnet.pe.kr/2/0/11632
따라서, 카메라를 적절하게 나무 옆으로 이동해 바라보면,
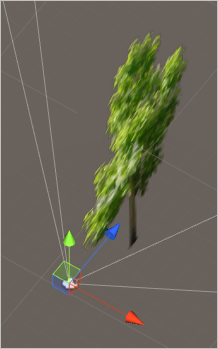
나무가 얇은 판 위에 그려진 것에 불과하기 때문에 다음과 같이 보이게 됩니다.

이럴 때, 만약 Plane 3D 객체를 카메라 방향으로 회전시켜주면 어떨까요?

그럼, 사용자가 y-축을 기준으로 x-z 평면에서 카메라를 이리저리 돌리며 봐도 다음과 같이 나무로 볼 수 있게 됩니다.

바로 이렇게 구현한 객체를 "빌보드(billboard)"라고 합니다.
그럼, 이 빌보드를 shader로 구현해 볼까요? ^^
어차피, x-z 평면에서 돌아다니는 거라면 y-축에 대해 카메라와 물체가 이루는 각을 구하고 그만큼 회전을 시켜주면 됩니다. 3차원 상에서의 두 점이 이루는 각은 이미 다음의 글에서 아크탄젠트를 이용해 구하는 방법을 설명했습니다.
3D 공간에서 두 점이 이루는 각도 구하기
; https://www.sysnet.pe.kr/2/0/11636
그리고 shader 내에서 World Matrix를 구하는 것도 설명했으니,
Unity - shader의 World matrix(unity_ObjectToWorld)를 수작업으로 구성
; https://www.sysnet.pe.kr/2/0/11633
Unity - World matrix(unity_ObjectToWorld)로부터 TRS(이동/회전/크기) 행렬로 복원하는 방법
; https://www.sysnet.pe.kr/2/0/11637
Unity - World matrix(unity_ObjectToWorld)로부터 Position, Rotation, Scale 값을 복원하는 방법
; https://www.sysnet.pe.kr/2/0/11640
이것을 이용하면 다음과 같이 shader 코드를 작성할 수 있습니다.
v2f vert(appdata v)
{
v2f o;
float4x4 scaleMatrix; // Scale 행렬
vector sx = vector(unity_ObjectToWorld._m00, unity_ObjectToWorld._m10, unity_ObjectToWorld._m20, 0);
vector sy = vector(unity_ObjectToWorld._m01, unity_ObjectToWorld._m11, unity_ObjectToWorld._m21, 0);
vector sz = vector(unity_ObjectToWorld._m02, unity_ObjectToWorld._m12, unity_ObjectToWorld._m22, 0);
float scaleX = length(sx);
float scaleY = length(sy);
float scaleZ = length(sz);
scaleMatrix[0] = float4(scaleX, 0, 0, 0);
scaleMatrix[1] = float4(0, scaleY, 0, 0);
scaleMatrix[2] = float4(0, 0, scaleZ, 0);
scaleMatrix[3] = float4(0, 0, 0, 1);
float4 pos = v.vertex;
float4 worldPos = float4(mul(unity_ObjectToWorld, float4(0, 0, 0, 1)).xyz, 0);
float4 cameraPos = float4(_WorldSpaceCameraPos.xyz, 0);
vector cameraDir = cameraPos - worldPos;
float xAngle = atan2(cameraDir.z, cameraDir.y);
float yAngle = atan2(cameraDir.z, cameraDir.x);
float zAngle = atan2(cameraDir.x, cameraDir.y);
xAngle = -radians(90);
yAngle = -(radians(90) + yAngle);
zAngle = 0;
float4x4 rotationMatrix = GetRotationMatrix(xAngle, yAngle, 0);
float4x4 moveMatrix;
moveMatrix[0] = float4(1, 0, 0, unity_ObjectToWorld._m03);
moveMatrix[1] = float4(0, 1, 0, unity_ObjectToWorld._m13);
moveMatrix[2] = float4(0, 0, 1, unity_ObjectToWorld._m23);
moveMatrix[3] = float4(0, 0, 0, 1);
float4x4 transformMatrix = mul(mul(moveMatrix, rotationMatrix), scaleMatrix);
pos = mul(transformMatrix, pos);
o.pos = mul(UNITY_MATRIX_VP, pos);
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
return o;
}
지난 글과 달라진 점은, rotationMatrix를 Unity 에디터의 Transform에서 설정한 값을 쓰지 않고 직접 설정했다는 점입니다.
float4 pos = v.vertex;
float4 worldPos = float4(mul(unity_ObjectToWorld, float4(0, 0, 0, 1)).xyz, 0);
float4 cameraPos = float4(_WorldSpaceCameraPos.xyz, 0);
vector cameraDir = cameraPos - worldPos;
float xAngle = atan2(cameraDir.z, cameraDir.y);
float yAngle = atan2(cameraDir.z, cameraDir.x);
float zAngle = atan2(cameraDir.x, cameraDir.y);
xAngle = -radians(90);
yAngle = -(radians(90) + yAngle);
zAngle = 0;
float4x4 rotationMatrix = GetRotationMatrix(xAngle, yAngle, 0);
왜냐하면, 보통 빌보드로 사용될 mesh는 Plane 객체이기 때문이고 이 객체는 생성 시 x-z 평면 상에 누워있기 때문입니다. 따라서, 이 Plane 객체를 세우기 위해 xAngle은 무조건 -90도를 설정했습니다.
xAngle = -radians(90);
y-축의 변화는 카메라와 물체가 이루는 각에 따라 달라지므로
두 점 간의 각도를 구하고 이에 따라 반응하도록 yAngle을 설정합니다.
yAngle = -(radians(90) + yAngle);
마지막으로 z-축은 빌보드가 어차피 3차원 이미지를 렌더링하는 용도는 아니므로 x-z 평면 상에서만 잘 동작하면 되기 때문에 0으로 설정합니다.
(
첨부 파일은 빌보드 구현 shader 전체 코드입니다.)
shader뿐만 아니라 C# 스크립트로도 빌보드를 구현할 수 있습니다. 나무 객체에 스크립트를 얹고 카메라가 있는 방향으로 회전을 시켜주면 되는데, 다음의 글은 이에 대해 설명하고 있습니다.
유니티3D, 게임 오브젝트를 특정 대상을 바라보게 하기
; http://legacy.tistory.com/81
처음부터 만들어 볼까요? ^^
우선, Plane 3D 객체를 놓고 texture를 보여줄 수 있는 shader를 얹으면
지난 글에 설명한 것처럼 바닥에 누워있는 평면이 생깁니다. 어차피 스크립트를 통해 회전시킬 것이기 때문에 이번에는 지난번처럼 material의 Texture 설정이나 x-축을 기준으로 한 회전을 미리 해둘 필요가 없습니다. 그다음 아래의 스크립트를 적용하면,
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class rotatePlane : MonoBehaviour
{
public Transform Camera;
void Start()
{
}
void Update()
{
if (Camera != null)
{
this.transform.LookAt(Camera);
}
}
}
여전히 누워 있는 상태는 변함이 없지만 이번에는 지난 글과는 다르게 누워 있는 나무의 방향이 반대입니다.
[그림: 좌측 - LookAt 적용 후, 우측 - LookAt 적용 전]

이 때문에 나무를 세우기 위해서 전에는 -90도를 했지만, 이번에는 +90도를 하면 됩니다.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class rotatePlane : MonoBehaviour
{
public Transform Camera;
void Start()
{
}
void Update()
{
if (Camera != null)
{
this.transform.LookAt(Camera);
this.transform.Rotate(Vector3.right * 90);
}
}
}
이렇게 하고 실행하면 마치 달이 지구를 바라보듯이 해당 물체는 카메라의 움직임에 따라 언제나 보이는 위치로 회전을 하게 됩니다. 위의 방법에서는 z-축을 기반으로 xy 평면 상에서 카메라를 움직여도 나무가 서 있는 효과가 납니다. 하지만 그렇다고 해서 이것이 2차원 평면이 가진 빌보드의 제약을 해결한 것은 아닙니다. 일례로, y-축으로 카메라를 이동해 하늘에서 바닥을 내려다본다고 했을 때 나무가 도로와 수직으로 서 있는 모습이 아닌, 도로와 평행으로 깔려 있는 모습으로 렌더링되기 때문입니다. 게다가, y-축의 정점을 지나는 경우 나무가 거꾸로 회전하는 변화도 거슬립니다. 결국, 빌보드는 모든 3차원 공간에서의 카메라 이동 용으로는 부적합하다는 것을 인정해야 합니다.
검색해 보면, 빌보드를 색다른 방식으로 구현한 shader 소스 코드를 찾을 수 있습니다.
kaiware007/billboard.shader
; https://gist.github.com/kaiware007/8ebad2d28638ff83b6b74970a4f70c9a
v2f vert (appdata v)
{
v2f o;
o.pos = UnityObjectToClipPos(v.vertex);
o.uv = v.uv;
// billboard mesh towards camera
float3 vpos = mul((float3x3)unity_ObjectToWorld, v.vertex.xyz);
float4 worldCoord = float4(unity_ObjectToWorld._m03, unity_ObjectToWorld._m13, unity_ObjectToWorld._m23, 1);
float4 viewPos = mul(UNITY_MATRIX_V, worldCoord) + float4(vpos, 0);
float4 outPos = mul(UNITY_MATRIX_P, viewPos);
o.pos = outPos;
UNITY_TRANSFER_FOG(o,o.vertex);
return o;
}
분석해 보면 이렇습니다. 아래의 연산을 통해 Unity Editor의 Inspector 창에 설정된 Rotation, Scale 관련한 행렬을 분리해,
float3x3 rsMatrix = (float3x3)unity_ObjectToWorld;
현재 vertex의 xyz 값을 곱하면서 위치 이동 없이 회전과 크기만 변한 상태의 vertex 위치를 구해둡니다.
float3 vpos = mul(rsMatrix, v.vertex.xyz);
그다음 unity_ObjectToWorld로부터 Position 좌표를 가져오고 있지만,
float4 worldCoord = float4(unity_ObjectToWorld._m03, unity_ObjectToWorld._m13, unity_ObjectToWorld._m23, 1);
사실 위의 코드는 다음과 같이 풀어서 이해할 수 있습니다.
float4x4 worldMatrix;
worldMatrix[0] = float4(1, 0, 0, unity_ObjectToWorld._m03);
worldMatrix[1] = float4(0, 1, 0, unity_ObjectToWorld._m13);
worldMatrix[2] = float4(0, 0, 1, unity_ObjectToWorld._m23);
worldMatrix[3] = float4(0, 0, 0, 1);
float4 objectCenterPosition = float4(0, 0, 0, 1); // 모델의 중심 값을 기준으로,
float4 worldCoord = mul(worldMatrix, objectCenterPosition); // 위치 이동한 좌표를 구하고,
즉, 모델의 중심 좌표에 대해 World 좌표계에 이동한 위치를 구한 것입니다. 이렇게 위치 이동한 것을 카메라 좌표계 기준으로 옮겨 준 다음,
float4 viewCenterPos = mul(UNITY_MATRIX_V, worldCoord);
카메라 좌표계에서의 중심점을 기준으로 회전/크기 변경된 vertex의 위치를 오프셋 연산합니다.
float4 viewPos = viewCenterPos + float4(vpos, 0);
따라서, 원래 Unity Editor의 Scene 화면에서 보이는 모습 그대로 카메라의 이동에 관계없이 그대로 보이게 되는 것입니다. 마지막으로 2차원 화면에 투영해 주는 것으로 끝!
float4 outPos = mul(UNITY_MATRIX_P, viewPos);
따라서 이 방법은 카메라의 좌표에 따라 회전하지 않기 때문에 스크립트로 LookAt + Rotate한 것과 비교해 다른 동작을 합니다. 아래의 화면을 보면,

좌측의 나무는 shader에서 한 것으로 카메라 위치가 바뀌어도 한결같이 정면을 바라보며 있습니다. 하지만 우측의 나무는 LookAt + Rotate한 것이기 때문에 회전을 하게 되고 나무의 밑동을 보면 방향을 틀은 것을 볼 수 있습니다. 실제로 2개의 방식을 혼용하면 이질적으로 동작하므로 하나로 통일하는 것이 좋습니다.
참고로, shader의 내장 변수 중 UNITY_MATRIX_IT_MV의 구성이 재미있습니다.
Built-in shader variables
; https://docs.unity3d.com/Manual/SL-UnityShaderVariables.html
UNITY_MATRIX_IT_MV - Inverse transpose of model * view matrix.
이 행렬로부터 카메라의 Up 벡터와 카메라의 시선이 향하는 방향 벡터를 다음과 같이 구할 수 있습니다.
Camera Up vector in vertex shader.
; https://forum.unity.com/threads/camera-up-vector-in-vertex-shader.144635/
float3 upvec = UNITY_MATRIX_IT_MV[1].xyz;
float3 viewDir = UNITY_MATRIX_IT_MV[2].xyz;
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]