Matlab/Octave로 Gram-Schmidt 정규 직교 집합 구하는 방법
a 행렬을 정의하고,
a = [1,1,0; 0,1,2; 1,2,1]'
a =
1 0 1
1 1 2
0 2 1
matlab/octave로 QR 분해하면 다음과 같은 결과가 나옵니다.
[q,r] = qr(a)
q =
-0.70711 0.23570 0.66667
-0.70711 -0.23570 -0.66667
-0.00000 -0.94281 0.33333
r =
-1.41421 -0.70711 -2.12132
0.00000 -2.12132 -1.17851
0.00000 0.00000 -0.33333
참고로, wolframalpha 웹 사이트에서 확인하면 실수 계산 값이 아닌 분수 형태의 값으로 구할 수 있습니다. (단지, 부호가 반대입니다.)
gram schmidt {{1,0,1},{1,1,2},{0,2,1}}
; http://m.wolframalpha.com/input/?i=gram+schmidt+%7B%7B1%2C1%2C0%7D%2C%7B0%2C1%2C2%7D%2C%7B1%2C2%2C1%7D%7D&x=0&y=0
1/sqrt(2), -1/(3*sqrt(2)), -2/3
1/sqrt(2), 1/(3*sqrt(2)) , 2/3
0 , 2*sqrt(2) / 3 , -1/3
여기서, Q 결괏값은 직교 행렬로 X
i * X
j = 0 (i != j)인 조건을 만족합니다. 검증은 다음과 같이 쉽게 할 수 있습니다.
# a1 = [-0.70711, -0.70711, 0]
# a2 = [0.23570, -0.23570, -0.94281]
# a3 = [0.66667, -0.66667, 0.33333]
a1 = q(:,1)'
a2 = q(:,2)'
a3 = q(:,3)'
>> dot(a1, a2)
ans = 0
>> dot(a2, a3)
ans = 1.3807e-006 // 실수 계산 값의 오차 누적으로 인한 것일 뿐 0 값임!
>> dot(a3, a1)
ans = 0
또한, Q 결괏값은 정규 직교 행렬이기 때문에 X
i * X
j = 1 (i == j)인 조건을 만족하고, 이는 norm의 값이 1이므로 다음과 같이 검증할 수 있습니다.
>> dot(a1,a1)
ans = 1.0000
>> norm(a1)
ans = 1.0000
// 이하 a2, a3에 대해서도 동일한 결괏값
QR 분해의 Q 행렬은 Gram-Schmidt 정규 직교화 과정에 해당하기 때문에 다음과 같이 수작업으로도 구할 수 있습니다.
a1 = [1,1,0]
na1 = norm(a1)
ea1 = a1 / na1 // 계산 값: 0.70711, 0.70711, 0
a2 = [0,1,2]
_a2 = a2 - dot(a2,ea1) * ea1
n_a2 = norm(_a2)
ea2 = _a2 / n_a2 // 계산 값: -0.23570 0.23570 0.94281
a3 = [1,2,1]
_a3 = a3 - dot(a3,ea1) * ea1 - dot(a3,ea2) * ea2
n_a3 = norm(_a3)
ea3 = _a3 / n_a3 // 계산 값: -0.66667 0.66667 -0.33333
재미있는 것은, 직접 계산한 값의 경우에도 부호는 wolframalpha의 것과 같은 반면 matlab/octave의 QR 함수와는 반대입니다. (혹시 이 이유를 알고 계신 분은 덧글 부탁드립니다. ^^)
실제로 이런 수작업을 별도의 함수로 구현하고 그것이 matlab/octave의 qr 함수와 같다는 것을 다음의 문서에서 정리하고 있습니다.
The Gram-Schmidt process in Matlab
; https://www.math.purdue.edu/~wang838/teaching/GramSchmidt.pdf
기왕 해본 김에 octave 명령어도 알아볼 겸, 정규 직교 집합을 시각화해보겠습니다.
a1 = [1,1,0]'
a2 = [0,1,2]'
a3 = [1,2,1]'
a = [a1 a2 a3]
[q,r] = qr(a)
ad1 = quiver3(0,0,0,-q(1),-q(2),-q(3))
hold on
ad2 = quiver3(0,0,0,-q(4),-q(5),-q(6))
hold on
ad3 = quiver3(0,0,0,-q(7),-q(8),-q(9))
hold on
axis equal
text(-q(1),-q(2),-q(3), 'ad1')
text(-q(4),-q(5),-q(6), 'ad2')
text(-q(7),-q(8),-q(9), 'ad3')
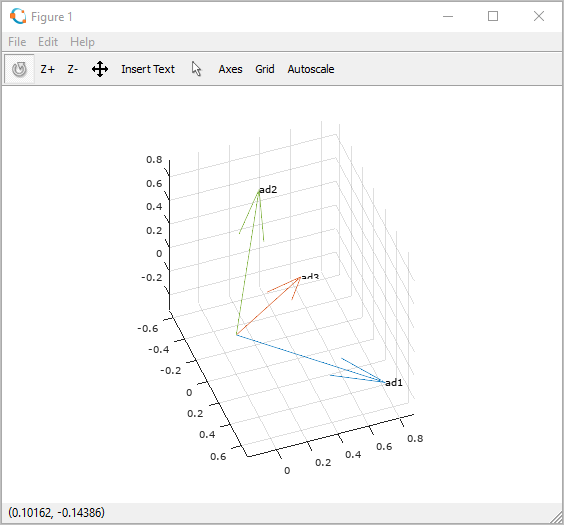
그럼, 다음과 같은 결과를 얻을 수 있고 "Rotate" 기능을 이용해 마우스로 이리저리 돌려 보면 3개의 벡터가 직교하고 있음을 눈으로 쉽게 확인할 수 있습니다.
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]