3D 공간에서 두 점이 이루는 각도 구하기
예를 들어, 다음과 같이 3D 공간에서 면과 점이 있다고 가정해 보겠습니다.
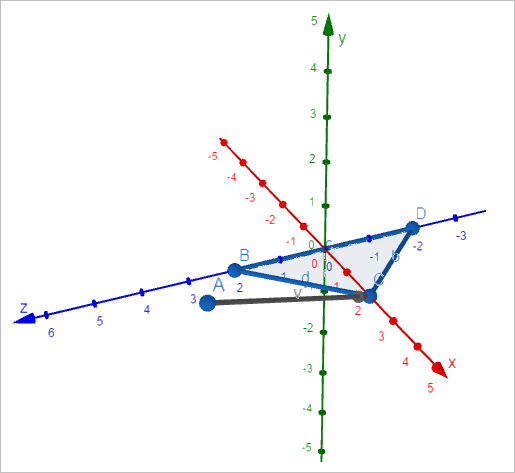
(오른손 좌표계 시스템의 x-y-z 축을 사용하고 있습니다.)
이때 점 C와 점 A가 이루는 각도는 어떻게 될까요? 간단하게 점과 점의 위치를 빼서 벡터를 만들고,
점 C와 카메라의 벡터 = 점 C - 점 A
= (-1.4, -2.9, -5)
그 벡터가 이루는 각을 3차원에 따라 각 축 별로 3개의 각도를 구할 수 있습니다.
- x-축을 기준으로 y-z 평면의 각
- y-축을 기준으로 x-z 평면의 각
- z-축을 기준으로 x-y 평면의 각
역시 시각화를 해보는 게 좋겠지요? ^^ GeoGebra 앱에서 "Home" 모양의 아이콘을 누르면,
차례대로 "y축을 기준으로 x-z 평면", "z축을 기준으로 x-y 평면", "x축을 기준으로 y-z 평면" 상에서의 물체를 볼 수 있는 기능이 제공됩니다.
자... 멋진 툴이 있으니, 그럼 우선 첫 번째 아이콘인 "y축을 기준으로 x-z 평면"을 다음과 같이 볼 수 있습니다. ^^
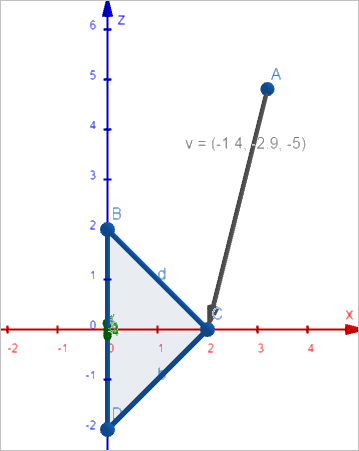
보는 바와 같이 x-z 평면에서 벡터가 이루는 각을 쉽게 확인할 수 있습니다. 점 A에서 x-축으로 수선의 발을 그렸을 때,
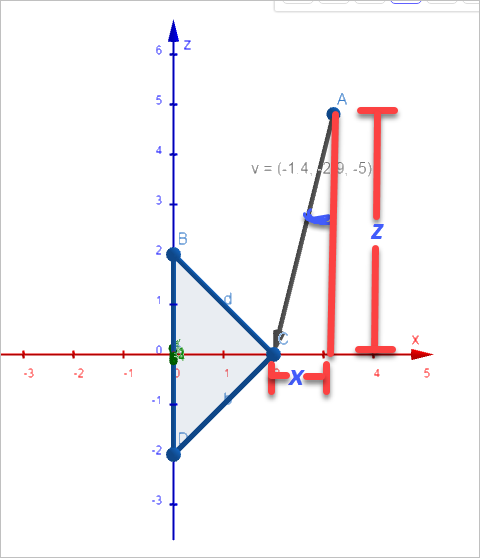
직각 삼각형이 되고 이때 우리가 아는 벡터 A의 x, z 성분의 값으로 인해 아크 탄젠트 함수를 사용하면 점 A에서 이루는 각도를 구할 수 있습니다.
각 A = arc_tangent(vx, vz);
C# 코드로 구해 보면 다음과 같습니다.
Vector3 v3 = new Vector3(-1.4f, -2.9f, -5f);
{
double yAngle = Math.Atan2(v3.X, v3.Z);
Console.WriteLine(RadianToDegree(yAngle));
}
실행해 보면, -164.357753796137도가 나오는데, 벡터가 음의 방향이어서 그런 것일 뿐 180도를 빼면 약 15.6도가 나옵니다. 동일한 각도를 Geogebra 기하를 이용해서도 구해 볼까요? ^^
2차원 좌표계에서 x, z의 성분으로 점을 표시한 후 그와 연결한 벡터를 그리고 그
사잇각을 다음과 같이 구할 수 있습니다.
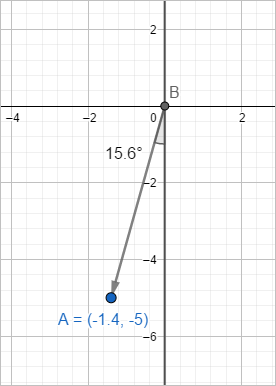
잘 맞아 들어가는군요. ^^
마찬가지 방식으로 "z축을 기준으로 x-y 평면"과,
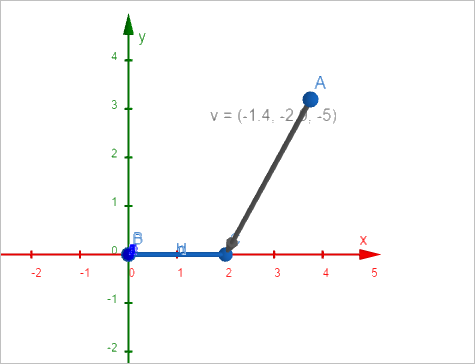
"x축을 기준으로 y-z 평면" 상의 모습을 확인하며,
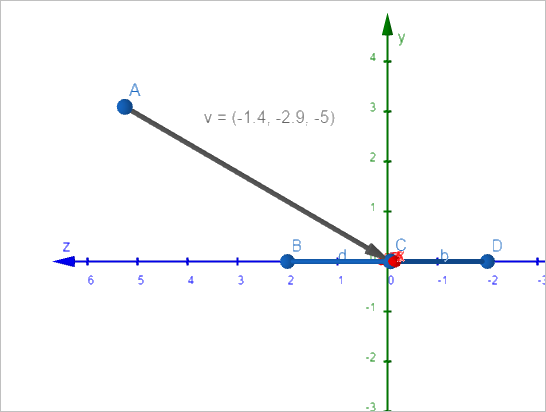
각도를 구해 보면 이렇습니다.
Vector3 v3 = new Vector3(-1.4f, -2.9f, -5f);
Console.WriteLine("xAngle");
{
double xAngle = Math.Atan2(v3.Y, v3.Z);
Console.WriteLine(RadianToDegree(xAngle));
}
Console.WriteLine("yAngle");
{
double yAngle = Math.Atan2(v3.X, v3.Z);
Console.WriteLine(RadianToDegree(yAngle));
}
Console.WriteLine("zAngle");
{
double zAngle = Math.Atan2(v3.Y, v3.X);
Console.WriteLine(RadianToDegree(zAngle));
}
/*
출력 결과
xAngle
-149.886266031276
yAngle
-164.357753796137
zAngle
-115.769326504636
*/
(
첨부 파일은 이 글에서 예제로 사용한 geogebra 파일입니다.)
참고로, 2개의 벡터가 이루는 각은 아크코사인을 이용해 구할 수 있습니다.
vector v1 = ...;
vector v2 = ...;
vector nv1 = normalize(v1);
vector nv2 = normalize(v2);
float angle = acos(mul(nv1, nv2));
일반적으로 acos의 정의역이 -1 ~ 1이기 때문에 정규화된 벡터의 내적 연산으로 NaN 값을 반환하는 경우는 없습니다. 문제는 0 벡터인 경우 normalize 하는 과정에서 NaN이 나온다는 것입니다.
vector v = vector(0, 0, 0, 0);
vector normal = normalize(v); // normal == NaN
왜냐하면 정규화라는 것이 벡터 크기로 나누는 것인데,
${
\hat v = \left ( \frac{ v_x }{ \Vert v \Vert }, \frac{ v_y }{ \Vert v \Vert }, \frac{ v_z }{ \Vert v \Vert } \right )
}$
분모가 0이 되므로 normalize의 결과가 NaN이 나옵니다. 이 때문에 mul 연산도 NaN이 되고, acos까지 NaN으로 끝납니다.
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]