임의 축을 기반으로 3D 벡터 회전
아래의 질문을,
벡터에 대한 질문입니다.
; http://lab.gamecodi.com/board/zboard.php?id=GAMECODILAB_QnA_etc&no=5615&z=
정리해 보면 다음과 같은 식으로 정점 3개가 있을 때 나머지 하나의 정점 위치를 정하는 것입니다.
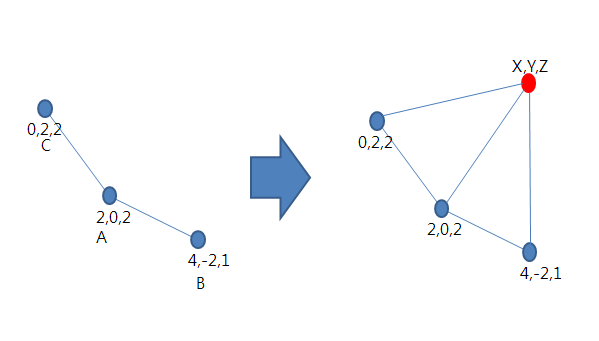
A = [2 0 2]
B = [4 -2 1]
C = [0 2 2]
D = ?
그냥 생각해 보면 대략 3가지 정도의 정점 위치를 정할 수 있을 것 같습니다.
- 폴리곤 ABC와 대칭인 BCD를 정하는 위치
- 선분 BC의 길이를 이등분한 연장선 위에 선분 AB 또는 선분 AC의 길이만큼 떨어진 위치
- 각 CAB를 이등분한 연장선 위에 선분 AB 또는 선분 AC의 길이만큼 떨어진 위치
하나씩 해볼까요? ^^ 우선 대칭인 위치를 잡는 것은 2D 기준일 때 다음과 같은 식이 됩니다.
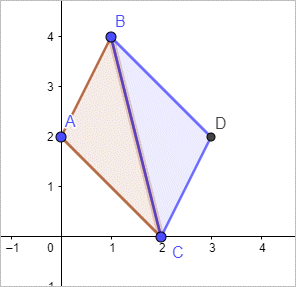
그리고 이 위치는 코딩하기도 편합니다. 단순히 벡터 AB와 벡터 AC를 더하면 되기 때문입니다.
v1 = B - A
v2 = C - A
v3 = v1 + v2
D = A + v3
위의 계산은 2D, 3D 공간에 상관없이 적용할 수 있습니다.
첫 번째 것은 해결했으니 이제 그다음 방법으로 넘어가겠습니다. 작도로 풀어보면 다음과 같이 선분 BC의 길이를 이등분한 후 선분 AB 또는 선분 AC의 길이 중 긴 것을 기준으로 위치를 잡으면 됩니다. (짧은 것을 기준으로 하면 선분 AE의 안쪽에 D가 위치할 경우가 나옵니다.)
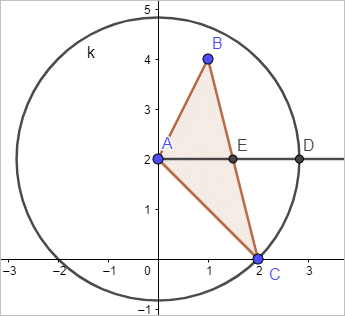
이것을 벡터 계산으로 Octave에서 계산해 보면 다음과 같습니다.
# Octave script
A = [2 0 2];
B = [4 -2 1];
C = [0 2 2];
half_bc = (B - C) / 2
midPt = C + half_bc
aDirection = midPt - A
u = aDirection / norm(aDirection)
if (norm(A - C) > norm(A - B))
lt = norm(A - C)
else
lt = norm(A - B)
endif
ut = u * lt
A + ut
시각화를 위해 GeoGebra 프로그램으로 보면 이렇게 폴리곤 구성이 됩니다.
# Geogebra equation
A= (2,0,2)
B= (4,-2,1)
C= (0,2,2)
half= (B-C)/(2)
MIDPT=C+half
adirect=MIDPT-A
u=(adirect)/(abs(adirect))
LT=If(abs(A-C)>abs(A-B),abs(A-C),abs(A-B))
ut=u*LT
D=A+ut
Polygon(A, B, C)
Polygon(C, D, B)
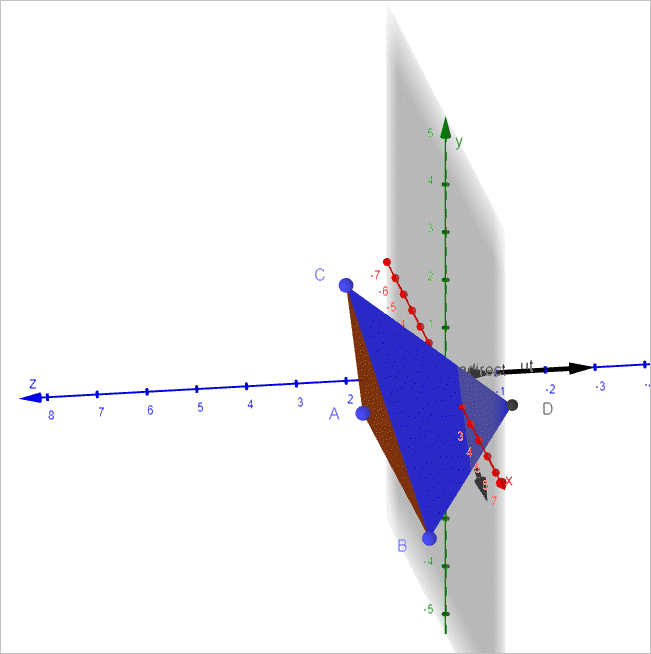
자, 이제 마지막 방법인 "각 CAB를 이등분한 연장선 위에 선분 AB 또는 선분 AC의 길이만큼 떨어진 위치"를 잡아보겠습니다. 이번에는 좀 쉽지 않습니다. 우선, 각 CAB를 이등분한 값을 얻어야 하는데요. 이것은 두 벡터의 각을 구하는 공식을 사용해 해결할 수 있습니다.
두 직선, 벡터의 관계(사이각,회전각) 구하기
; http://darkpgmr.tistory.com/121
따라서 Octave 스크립트 상으로는 다음과 같이 코딩할 수 있습니다.
A = [2 0 2];
B = [4 -2 1];
C = [0 2 2];
v1 = B - A
v2 = C - A
THETA = acos(dot(v1, v2) / (norm(v1) * norm(v2))) / 2
# rad2deg(THETA)
각을 구했으니, 이제 벡터 v1이나 벡터 v2 중에 길이가 긴 선분을 그 각도만큼 회전시키면 점 D의 위치를 결정할 수 있습니다. 문제는, 이때의 회전은 지난 글에서 알아본 x-y 평면, y-z 평면, x-z 평면의 회전 방정식과는,
Unity - World matrix(unity_ObjectToWorld)로부터 Position, Rotation, Scale 값을 복원하는 방법
; https://www.sysnet.pe.kr/2/0/11640
${
Rx = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos \theta & -sin \theta & 0 \\ 0 & sin \theta & cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
}$
${
Ry = \begin{bmatrix} cos \theta & 0 & sin \theta & 0 \\ 0 & 1 & 0 & 0 \\ -sin \theta & 0 & cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
}$
${
Rz = \begin{bmatrix} cos \theta & -sin \theta & 0 & 0 \\ sin \theta & cos \theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
}$
무관하다는 점입니다. 즉, 위의 회전 행렬식들은 각각의 평면에 대해 x, y, z 축을 기준으로 삼는데, 이 글에서 설명한 폴리곤 ABC는 별도의 평면을 이루기 때문입니다.
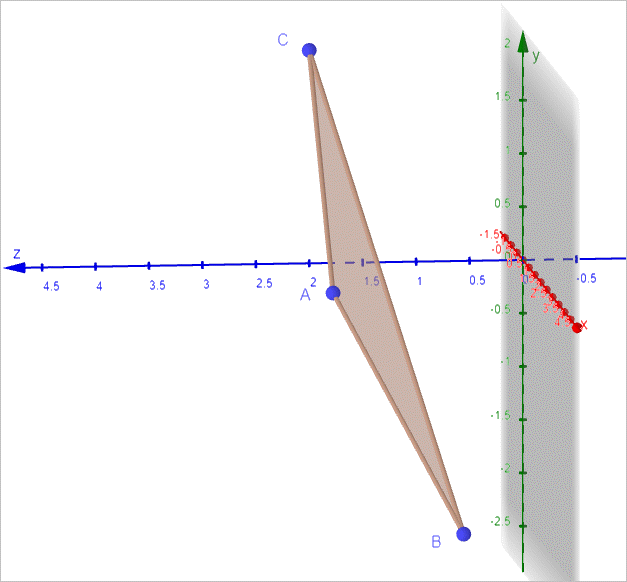
따라서 저 평면을 기준으로 수직인 축을 정해 그것을 기반으로 회전을 해야 하는데, 다행히 이에 대해서는 ^^ 멋있는 수학자들이 이미 잘 풀어서 설명해 놓았습니다.
임의의 축 회전 (Axis Angle Rotation)
; http://nobilitycat.tistory.com/entry/%EC%9E%84%EC%9D%98%EC%9D%98-%EC%B6%95-%ED%9A%8C%EC%A0%84-Axis-Angle-Rotation
임의 방향의 회전에 대한 회전 행렬 공식의 유도
; http://spacebug.blog.me/130187075488
${
\begin{bmatrix} x' \\ y' \\ z' \end{bmatrix}
}$
${
= \begin{bmatrix} w_x^2 (1 - cos \alpha) + cos \alpha & w_x w_y (1 - cos \alpha) + w_z sin \alpha & w_x w_z (1 - cos \alpha) - w_y sin \alpha \\ w_y w_x (1 - cos \alpha) - w_z sin \alpha & w_y^2 (1 - cos \alpha) + cos \alpha & w_y w_z (1 - cos \alpha) + w_x sin \alpha \\ w_z w_x (1 - cos \alpha) + w_y sin \alpha & w_z w_y (1 - cos \alpha) - w_x sin \alpha & w_z^2 (1 - cos \alpha) + cos \alpha \end{bmatrix}
}$
${
\begin{bmatrix} x \\ y \\ z \end{bmatrix}
}$
따라서, octave 스크립트 코드를 다음과 같이 마저 완성할 수 있습니다.
# test
A = [2 0 2];
B = [4 -2 1];
C = [0 2 2];
v1 = B - A
v2 = C - A
THETA = acos(dot(v1, v2) / (norm(v1) * norm(v2))) / 2
# rad2deg(THETA)
rotAxis = cross(v1, v2)
uRotAxis = rotAxis / norm(rotAxis)
WX = uRotAxis(1);
WY = uRotAxis(2);
WZ = uRotAxis(3);
MCOS = 1 - cos(THETA);
COSA = cos(THETA);
SINA = sin(THETA);
M11 = WX * WX * MCOS + COSA;
M12 = WX * WY * MCOS + WZ * SINA;
M13 = WX * WZ * MCOS - WY * SINA;
M21 = WY * WX * MCOS - WZ * SINA;
M22 = WY * WY * MCOS + COSA;
M23 = WY * WZ * MCOS + WX * SINA;
M31 = WZ * WX * MCOS + WY * SINA;
M32 = WZ * WY * MCOS - WX * SINA;
M33 = WZ * WZ * MCOS + COSA;
rotMatrix = [M11 M12 M13; M21 M22 M23; M31 M32 M33]'
aDirect = rotMatrix * v1'
u = aDirect / norm(aDirect)
if (norm(C - A) > norm(B - A))
LT = norm(C - A)
else
LT = norm(B - A)
endif
ut = u' * LT
D = A + ut
# D 좌표 == [1.64128 0.35872 -0.95680]
그리고 GeoGebra에서 위의 공식을 적용해 그려 보면 다음과 같은 결과를 얻을 수 있습니다.
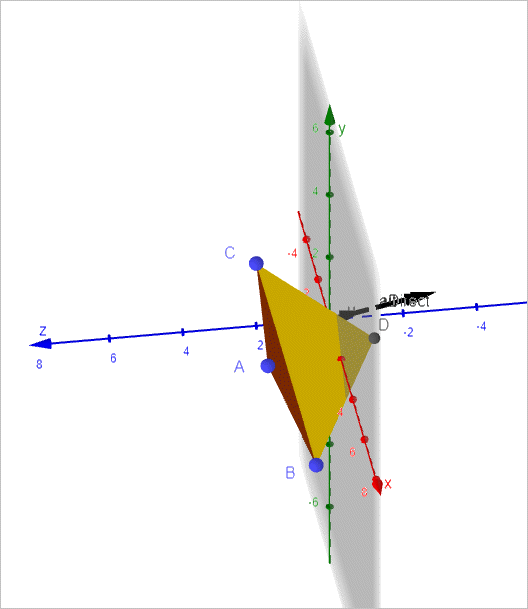
(
첨부 파일은 이 글의 Octave 스크립트 파일과 GeoGebra ggb 파일을 포함합니다.)
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]