황금비율 증명
(이 글의 내용에는 SVG 태그를 사용하고 있으므로, HTML5 지원 브라우저에서 보는 것이 좋습니다.)
황금비율 관련해서 책을 읽고 있는데요.
황금 비율의 진실: 완벽을 창조하는 가장 아름다운 비율의 미스터리와 허구
; http://www.yes24.com/24/goods/5266967?scode=032
^^ 나중을 위해 정리를 해두는 것이 좋을 것 같아서 이렇게 적어봅니다. ^^
1. 펜타그램에서 황금 비율 작도
지난번 글에서 펜타그램을 그려봤었는데요.
C# - 펜타그램(Pentagram) 그리기
; https://www.sysnet.pe.kr/2/0/1310
펜타그램의 선을 모두 잇지 말고 아래와 같이 이등변 삼각형에 대해서만 그어보겠습니다.
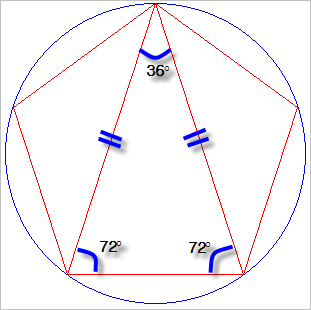
"원론"의 한 정리에 따른 두 삼각형에서 두 내각이 같으면 (삼각형은 3개의 내각을 가지고 있고 합이 180도이기 때문에 두 개가 같다는 것은 3개가 같다는 것과 같음) 이 두 삼각형은 서로 '닮음'이라고 합니다. 즉, 그 두 삼각형의 모양은 완전히 똑같고 단지 변들의 길이만 차이가 날 뿐입니다. 그리고, '닮은 삼각형'끼리는 모든 변들의 비율이 서로 같게 됩니다.
위에서 그려진 삼각형과 닮은 꼴의 삼각형을 다음과 같이 선을 긋는 것으로 생성할 수 있습니다.
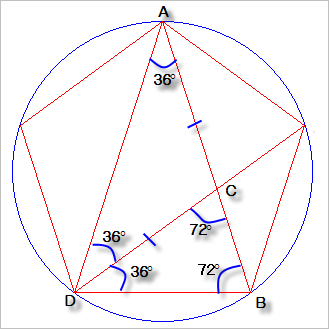
보시는 것처럼, 삼각형 ADB와 DBC는 내각의 조건에 의해서 서로 닮음입니다. 이 때문에, 삼각형 ADB의 선분 AB와 DB의 비율은 작은 삼각형 DBC의 선분 DB와 BC의 비율과 같게 됩니다.
AB/DB = DB/BC
여기서 삼각형 ADC를 볼 필요가 있습니다. 꼭지점 A, D의 각이 36도이기 때문에 이등변 삼각형이 되고 따라서 선분 AC와 선분 DC의 길이는 같습니다. 이어서, 삼각형 DBC도 이등변 삼각형이기 때문에 그것의 선분 DC와 DB의 길이는 같습니다. 따라서 다음의 공식이 성립합니다.
AC = DC = DB
결국, 위의 2가지 등식은 다음과 같이 정리될 수 있습니다.
AC/BC = AB/AC
위의 정리된 비율을 선분으로 정리하면 다음과 같습니다. (아래의 svg 내의 수치는 황금비에 맞추지 않고 대강 그린 것이므로 가져다 쓰실 때 주의하세요. ^^)
위에서 하나의 단일 선분에서 중간에 점 C를 기준으로 황금비를 나타냈는데요. 이에 대해서 유클리드는 다음과 같이 표현을 했습니다.
"직선 전체(AB)와 긴 선분(AC)의 비가 긴 선분(AC)과 짧은 선분(BC)의 비와 같을 때, 이 직선은 외중비에 따라 분할됐다고 말한다.
"
비율 공식으로 나타내면 다음과 같습니다.
AC:CB = AB:AC
좀 더 구체적인 공식으로 표현하려면, 짧은 선분 CB의 길이를 1로 놓으면 됩니다. 그럼 긴 선분 AC를 x로 놓고 x대 1의 비는 'x + 1'(직선 AB의 길이)대 x의 비와 같게 됩니다.
x / 1 = (x + 1) / x
양변을 풀어보면, x
2 = x + 1이 되며, 이것을 정리하면 다음과 같은 이차방정식이 됩니다.
x2 - x - 1 = 0
우리가 익히 잘 알고 있는 '근의 공식'에 따라 해는 다음과 같이 구해집니다.
x1 = (1 + √5) / 2,
x2 = (1 - √5) / 2
이 가운데 양의 해 = 1.6180339887...이 바로 황금수의 값 Φ(Phi)가 됩니다.
3. 숫자 1로 이뤄진 연분수의 값은 Φ(Phi)
다음의 연분수를 보면,
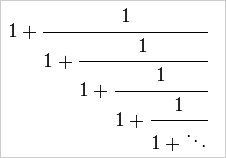
구하고자 하는 값을 x로 놓아 봅니다. 그럼, 둘째 항의 '분모'도 역시 'x'로 묶어 버릴 수가 있습니다.
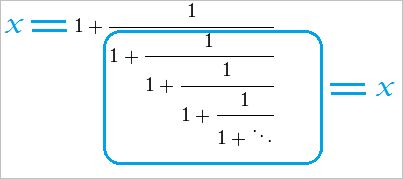
그래서 이를 정리하면 다음과 같은 공식이 나오고,
x = 1 + 1 / x
양변에 x를 곱해서 정리하면 전형적인 황금비 공식인 "x
2 = x + 1"가 되어, 결국 위의 연분수에 대한 값은 Φ(Phi)가 됩니다.
4. 숫자 1로 이뤄진 제곱근의 값은 Φ(Phi)
역시 1의 값으로 무한히 더해지는 제곱근의 공식을 보면,
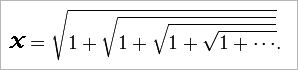
양변을 제곱해 보면, 다음과 같이 바뀝니다.
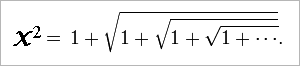
그런데, 우변의 1 이후의 값은 다시 기존 x 값으로 대체할 수 있으므로 결국 다음과 같은 공식으로 바뀝니다.
x2 = 1 + x
이번에도 역시 황금비 공식이고 그 해는 Φ(Phi)가 됩니다.
5. 피보나치 수와 연분수의 관계
피보나치 수열은 다들 아시는 것처럼 다음과 같이 이전 숫자의 합을 바탕으로 한 수열입니다.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...
이에 대해 앞의 수와의 비를 계산해 보면,
1/1 = 1.000000
2/1 = 2.000000
3/2 = 1.500000
5/3 = 1.666666
8/5 = 1.600000
13/8 = 1.625000
21/13 = 1.615385
34/21 = 1.619048
55/34 = 1.617647
89/55 = 1.618182
144/89 = 1.617978
233/144 = 1.618056
377/233 = 1.618026
610/377 = 1.618037
987/610 = 1.618033
피보나치 수열이 계속될 수록, (1 + √5) / 2로 구한 1.6180339887...에 가까워지는 것을 볼 수 있습니다. 이것이 우연일까요? 다시 연분수로 돌아가보겠습니다.
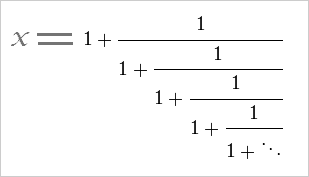
무한 연분수를 처음부터 하나씩 계산해 보면 그 수의 배열이 피보나치 수열과 일치하는 것을 볼 수 있습니다.
1 = 1.000000
1 + (1 / 1) = 2/1 = 2.000000
1 + (1 / (1 + 1)) = 3/2 = 1.500000
1 + 1 / (1 + 1 / (1 + 1)) = 5/3 = 1.66666
1 + 1 / (1 + 1 / (1 + 1 / (1 + 1))) = 8/5 = 1.60000
1 + 1 / (1 + 1 / (1 + 1 / (1 + 1 / (1 + 1)))) = 13/8 = 1.625000
황금수를 구하기 위한 연분수의 연속적인 근사값이 피보나치 수들의 비와 정확히 일치하는 것입니다.
기타 피보나치 수열과 황금 나선에 대해서 다음의 글에 그림이 실려 있습니다.
C# - 피보나치 수열의 사각형과 황금 나선(Golden spiral) 그리기
; https://www.sysnet.pe.kr/2/0/1311
첨언하자면,
황금 비율의 진실: 완벽을 창조하는 가장 아름다운 비율의 미스터리와 허구 책에서는 우리가 알고 있는 황금 비율이 얼마나 허구적으로 선전되었는가를 잘 파헤쳐 주고 있습니다. 수학적으로 아름다웠기 때문에 너도 나도 각종 논문이나 이야기 거리로 씌여지기 좋았고, 미술의 대가들이나 고대 신전들이 황금비를 따랐다는 말들이 얼마나 허구였는지를 일깨워 주고 있습니다.
위의 책에 실린 내용 중의 하나가, '사람들이 황금비로 이뤄진 사각형을 가장 선호한다'에 대해서 메인 대학교의 수학자 조지 마코스키(Markowsky, George)의 비공식적인 실험이 있습니다. 아래의 그림을 보여주면서 사람들에게 선택하라는 것이었는데요.

(from
Misconceptions about the Golden Ratio)
여러분들의 선택은 무엇인가요?
저는 위에서 3번째 줄에서 왼쪽으로부터 4번째 사각형을 선택했습니다. (진짜, 황금 직사각형은 네 번째 줄의 왼쪽에서 다섯 번째라고 합니다.)
'감수성의 신비감을 황금 분할로 대치하는 것'이라며 경계한 (그 자신은 황금비에 매혹되었으면서도) '르코르뷔지에(Le Corbusier)'의 의견이 어느 정도 공감이 됩니다.
끝으로... 이런 훌륭한 책을 소개해 준 ^^ 우리 회사의
전 지훈 과장님에게 감사를 드립니다.
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]