C# - (타)원 영역의 마우스 클릭 판단
아래와 같은 질문이 있어서 적어봅니다. ^^
동그란 형태의 영역 체크하기
; http://social.msdn.microsoft.com/Forums/ko-KR/visualcplusko/thread/ea521d3c-93ba-498f-860f-6fc689c1151d
우선, Win32 API로 CreateEllipticRgn, PtInRegion이 있기 때문에,
CreateEllipticRgn function
; https://docs.microsoft.com/en-us/windows/win32/api/wingdi/nf-wingdi-createellipticrgn
그리고, 영역 체크 역시 마찬가지입니다.
PtInRegion function
; https://docs.microsoft.com/en-us/windows/win32/api/wingdi/nf-wingdi-ptinregion
C#에서도 쉽게 DllImport 기능을 이용하여 사용할 수 있습니다.
그래도, 가끔은 원리를 아는 것이 중요할 때가 있지요. ^^ (가령, Javascript에서라면 Win32 API를 호출할 수 없기 때문에.)
우선, 원의 내부에서 마우스 클릭이 된 것인지 판단하는 것은 어렵지 않습니다.
아래 그림에서처럼,
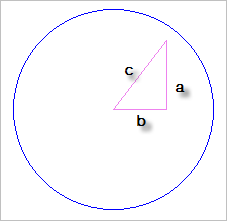
피타고라스 정리를 이용해서 c
2 = a
2 + b
2을 하게 되면 c의 길이를 구할 수 있고, 그 값이 반지름 r보다 작으면 원 안에 있다고 판단할 수 있습니다.
문제는 타원인데요. 이것은 타원에 대한 지식을 요구합니다.
타원 방정식
; http://yhsmc.com.ne.kr/Math/sunengdaebi/math2/sub3-8.pdf
타원은 "평면 위에서 두 정점에서의 거리의 합이 일정한 점 전체의 집합"이라고 정의되었는데요.
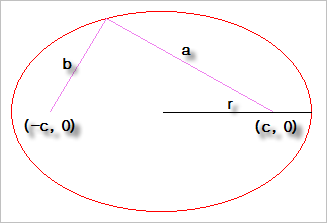
위의 그림에서 "두 정점"은 (-c, 0), (c, 0)을 의미하고, "거리의 합"은 2r, 즉 '장축'의 길이에 해당합니다. 따라서, 타원은 (-c, 0), (c, 0)을 잇는 선 a, b의 길이의 합이 2r인 '점 전체의 집합'이 됩니다.
여기서, 좌표 c는 무작위 값이 아니고 다음의 공식에 해당하는 좌표입니다.
c2 = a2 - b2
그럼, 기본적인 값은 모두 알아봤으니 이제 타원 내에 마우스가 위치해 있는 조건을 구할 수 있습니다. (위의 설명은 '장축 = x축, 단축 = y축'인 타원을 그렸을 때 해당하고, 그 반대의 경우라면 타원의 공식이 달라지기 때문에 그에 맞게 변경해 주어야 합니다.)
- 마우스 위치에 따른 b, a 길이는 피타고라스 정리에 의해서 구할 수 있고,
- b + a < 2r인 경우 타원 안에 있다고 판정.
첨부된 파일을 실행하면 다음과 같이 마우스 위치에 따라 "윈도우 타이틀" 속성에 True/False를 나타내는 예제가 동작합니다.
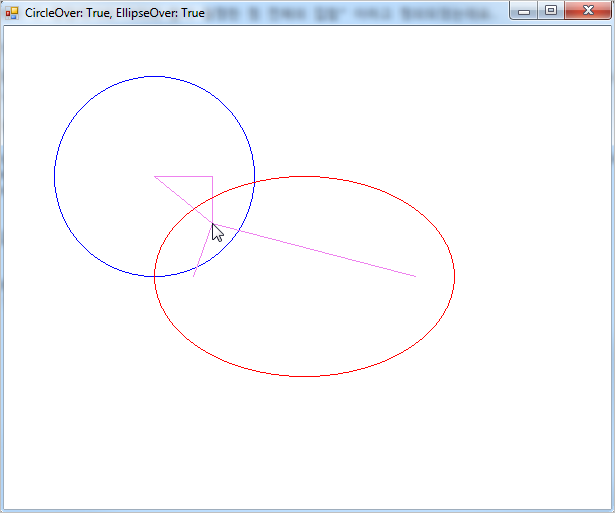
참고로, 예제 코드는 x, y의 장/단축이 바뀐 경우까지 반영되었습니다.
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]