C# - double (배정도 실수) 저장소의 비트 구조
double의 경우 지난 글에서 다룬 float 방식과 거의 같습니다.
C# - float (단정도 실수) 저장소의 비트 구조
; https://www.sysnet.pe.kr/2/0/13617
단지, 지수부와 가수부를 위한 비트 수만 좀 더 확장한 유형인데요, 다음의 그림에 따라,
[배정도 실수 - 그림 출처:
https://en.wikipedia.org/wiki/Double-precision_floating-point_format]
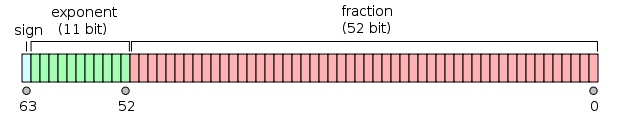
비트 구조만 맞춰서 masking만 잘하면 됩니다.
static unsafe void Main(string[] args)
{
double d = -118.625;
Console.WriteLine($"{d} (decimal: {(decimal)d}): sizeof(double): {sizeof(double)}");
Console.WriteLine();
byte* pDouble = (byte*)&d;
PrintDoubleFormat(pDouble);
}
private static unsafe void PrintDoubleFormat(byte* pDouble)
{
ulong data = *(ulong*)pDouble;
ulong signBitMask = 0b_1000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000;
ulong exponentMask = 0b_0111_1111_1111_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000;
ulong fractionMask = 0b_0000_0000_0000_1111_1111_1111_1111_1111_1111_1111_1111_1111_1111_1111_1111_1111;
ulong signBit = (data & signBitMask);
ulong exponentBits = (data & exponentMask);
ulong fractionBits = (data & fractionMask);
Console.WriteLine("signBit: \t" + Convert.ToString((long)signBit, 2).PadLeft(64, '0').Separator(4, '_'));
Console.WriteLine("exponentBits: \t" + Convert.ToString((long)exponentBits, 2).PadLeft(64, '0').Separator(4, '_'));
Console.WriteLine("fractionBits: \t" + Convert.ToString((long)fractionBits, 2).PadLeft(64, '0').Separator(4, '_'));
}
실행하면 다음과 같은 결과가 나오는데요,
-118.625 (decimal: -118.625): sizeof(double): 8
signBit: 1000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000
exponentBits: 0100_0000_0101_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000
fractionBits: 0000_0000_0000_1101_1010_1000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000
IEEE 754 표준에 따른 정규화 과정을 거쳐,
2진수 변환)
-118.625 ==> 1110110.101
지수 표현)
1110110.101 ==> 1.110110101 * 26
지수부: 6
가수부: 1.110110101
double의 경우 float와는 달리 exponentBits가 11비트로 늘었는데요, 따라서 0 ~ 2,047의 수를 표현할 수 있으니
bias 값이 1,023이 됩니다. 결국 지수부 6에 (float는 127을 더했지만) 1023을 더한 1029 값이 exponentBits(100 0000 0101)로 설정됩니다.
가수부의 처리도 비트만 52비트로 늘었을 뿐 float에서의 처리와 다르지 않습니다.
분해된 정보로부터 원래의 double 값을 복원하는 것도 float에서의 규칙과 같습니다. 가수부의 110110101에서 생략된 가장 상위의 1을 복원시키고,
1_1011_0101 ==> 11_1011_0101
그다음, 지수부의 1029를 원래의 지수로 만들어줍니다. (반대로 1023을 빼면 됩니다.)
6 = 1029 - 1023
이렇게 구한 값들을 통해 처음의 double 값으로 복원할 수 있습니다.
1.110110101 * 2E6
==> 1110110.101
10진수로 ==> 118.625
==> sign 비트 적용
-118.625
이 과정 역시
float의 코드를 조금만 바꾸면 double로 이렇게 만들 수 있고,
{
bool minus = signBit != 0;
ulong exponents = exponentBits >> 52;
// 삭제된 1을 복원하고,
ulong fractions = fractionBits | 0b_0000_0000_0001_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000;
int shift = (int)exponents - 1023;
// (삭제된 1로 인해 12비트가 아닌) 11비트만 shift 시키면 원래의 가수로 변환
fractions = fractions << 11;
string mantissa = Convert.ToString((long)fractions, 2).TrimEnd('0');
Console.WriteLine($"{(minus ? "-" : "")}{mantissa} * 2E{shift}");
mantissa = Convert.ToString((long)fractions, 2).TrimEnd('0');
mantissa = MarkDecimalPoint(mantissa, shift);
Console.WriteLine($"{(minus ? "-" : "")}{mantissa}");
decimal value = Recomposite(mantissa) * (minus ? -1 : 1);
Console.WriteLine($"{value}, (double: {(double)value})");
}
// ... 기타 코드는 float 예제와 동일 ...
이전 코드와 합쳐서 실행해 보면 이런 결과를 얻을 수 있습니다.
-118.625 (decimal: -118.625): sizeof(double): 8
signBit: 1000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000
exponentBits: 0100_0000_0101_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000
fractionBits: 0000_0000_0000_1101_1010_1000_0000_0000_0000_0000_0000_0000_0000_0000_0000_0000
-1110110101 * 2E6
-1110110.101
-118.625, (double: -118.625)
(
첨부 파일은 이 글의 예제 코드를 포함합니다.)
참고로, NaN과 infinity 처리도 있는데 이에 대해서는 전에 설명한 적이 있습니다.
C#, C++ - double의 Infinity, NaN 표현 방식
; https://www.sysnet.pe.kr/2/0/11896
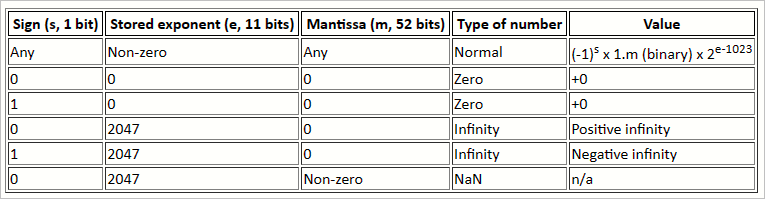
그런데 저렇게 장황하게 설명한 것보다 아래의 글에 도표로 잘 정리된 것이 있군요. ^^
Binary floating point and .NET
; https://csharpindepth.com/Articles/FloatingPoint
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]