Unity - shader의 Camera matrix(UNITY_MATRIX_V)를 수작업으로 구성
지난 글에서 월드 행렬을 수작업으로 구성해 봤으니,
Unity - shader의 World matrix(unity_ObjectToWorld)를 수작업으로 구성
; https://www.sysnet.pe.kr/2/0/11633
이번에는 View Matrix(Camera Matrix)를 수작업으로 구성해 보겠습니다. 다음의 책을 보면,
유니티로 배우는 게임 수학 기초 개념부터 모바일까지, 게임 개발에 필요한 수학 원리 설명서
; http://www.yes24.com/24/goods/30119802
View Matrix에 대한 구성 공식을 다음과 같이 소개하고 있습니다.
${
V = RT = \begin{bmatrix} X_x & X_y & X_z & 0 \\ Y_x & Y_y & Y_z & 0 \\ Z_x & Z_y & Z_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -C_x \\ 0 & 1 & 0 & -C_y \\ 0 & 0 & 1 & -C_z \\ 0 & 0 & 0 & 1 \end{bmatrix}
}$
위의 공식에서 X, Y, Z는 카메라의 회전 값이고 C는 카메라의 위치입니다. (View 행렬의 특성상 Scale 값은 무시합니다. 실제로 Unity의 Inspector 창에서 카메라의 Scale 값을 입력해도 아무런 변화가 없는 것을 볼 수 있습니다.)
예를 들어, 유니티 초기 카메라 좌표가 (0, 1, -10)입니다. 따라서 이대로 월드 좌표계 기준으로 보면 다음과 같은 Position을 갖도록 T(이동) 행렬을 구성할 수 있습니다.
float4x4 posView;
posView[0] = float4(1, 0, 0, -0);
posView[1] = float4(0, 1, 0, -1);
posView[2] = float4(0, 0, 1, -(-10));
posView[3] = float4(0, 0, 0, 1);
이것을 일반화하려면 Unity Shader에서 카메라의 위치를 나타내는 내장 변수인 _WorldSpaceCameraPos를 사용하면 됩니다.
float4x4 posView;
posView[0] = float4(1, 0, 0, -_WorldSpaceCameraPos.x);
posView[1] = float4(0, 1, 0, -_WorldSpaceCameraPos.y);
posView[2] = float4(0, 0, 1, -_WorldSpaceCameraPos.z);
posView[3] = float4(0, 0, 0, 1);
그다음, 카메라의 회전을 다뤄야 하는데요. 이게 좀 복잡합니다. 자세하게 들어가기 전 위의 posView가 정상적인 데이터를 가지고 있는지 다음과 같이 확인해 볼 수 있습니다.
float4x4 rotView;
float4x4 posView;
float4x4 viewMatrix;
posView[0] = float4(1, 0, 0, -_WorldSpaceCameraPos.x);
posView[1] = float4(0, 1, 0, -_WorldSpaceCameraPos.y);
posView[2] = float4(0, 0, 1, -_WorldSpaceCameraPos.z);
posView[3] = float4(0, 0, 0, 1);
float4x4 m = UNITY_MATRIX_V;
rotView[0] = float4(m[0].xyz, 0);
rotView[1] = float4(m[1].xyz, 0);
rotView[2] = float4(m[2].xyz, 0);
rotView[3] = float4(0, 0, 0, 1);
viewMatrix = mul(rotView, posView);
pos = mul(unity_ObjectToWorld, v.vertex);
pos = mul(viewMatrix, pos);
pos = mul(UNITY_MATRIX_P, pos);
V=RT 공식에서 보면 뷰 행렬의 경우 X, Y, Z의 회전 값이 V 행렬에 그대로 반영되기 때문에 위와 같이 UNITY_MATRIX_V로부터 회전 행렬 요소들을 구해올 수 있는 것입니다.
자, 그럼 이제 카메라의 회전 행렬 R을 구성하는 기저 벡터 X, Y, Z를 구해 보겠습니다. 이 방법에 대해서도 "
유니티로 배우는 게임 수학 기초 개념부터 모바일까지, 게임 개발에 필요한 수학 원리 설명서" 책에서 잘 설명해 주고 있습니다. 우선 Z 요소의 경우 다음과 같이 공식을 제시하고 있는데,
${
Z = { C - P \over |C - P| }
}$
여기서 C는 카메라의 위치이고 P는 카메라가 바라보는 시선의 끝점이라고 합니다. 그런데, C - P는 점과 점을 뺀 연산이기 때문에 vector입니다. 그리고 그 vector의 의미는 결국 View Direction이 되는 것입니다. 그러고 보니, view direction을 보관하고 있는 unity shader의 내장 변수를
지난 글에서 소개했습니다.
UNITY_MATRIX_IT_MV - Inverse transpose of model * view matrix.
vector viewDir = UNITY_MATRIX_IT_MV[2];
따라서 Z 값은 다음과 같이 구할 수 있습니다.
vector rorZ = normalize(viewDir);
그다음 기저 벡터 X는 위에서 구한 Z 벡터와 카메라의 상단을 향한 "up vector"를 외적해 구할 수 있습니다.
${
X = { U \times Z \over |U \times Z| }
}$
"up vector" 역시 UNITY_MATRIX_IT_MV[1]을 통해 구할 수 있으므로 다음과 같이 계산할 수 있습니다.
vector rorXpt = vector(cross(upvec, rorZ), 0);
float lenghX = length(rorXpt);
vector rorX = (rorXpt / lenghX);
// 또는,
vector rorX = normalize(vector(cross(upvec, rorZ), 0));
외적한 결과는 오른손 좌표계(RHS)인 경우에 해당하므로 왼손 좌표계(LHS)를 따르는 Unity를 위해 결괏값을 음수로 바꿔야 합니다.
vector rorX = -normalize(vector(cross(upvec, rorZ), 0));
X, Z에 대한 기저 벡터를 구했으니 나머지 Y에 대한 기저 벡터는 X, Z를 외적해서 구할 수 있습니다.
${
Y = { Z \times X \over |Z \times X| }
}$
따라서 shader에서는 다음과 같이 구할 수 있습니다. (마찬가지로 왼손 좌표계를 따르므로 외적의 결과에 음수 처리합니다.)
vector rorY = -normalize(vector(cross(rorZ, rorX), 0));
지금까지의 모든 결과를 취합하면 다음과 같이 수작업으로 구성한 View 행렬을 shader에서 사용할 수 있습니다.
Shader "Unlit/NewUnlitShader"
{
Properties
{
}
SubShader
{
Tags { "RenderType" = "Opaque" }
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
};
struct v2f
{
float4 vertex : SV_POSITION;
};
float4x4 _viewMatrix;
float4x4 _projectionMatrix;
v2f vert(appdata v)
{
float4 pos;
v2f o;
float4x4 rotView;
float4x4 posView;
float4x4 viewMatrix;
posView[0] = float4(1, 0, 0, -_WorldSpaceCameraPos.x);
posView[1] = float4(0, 1, 0, -_WorldSpaceCameraPos.y);
posView[2] = float4(0, 0, 1, -_WorldSpaceCameraPos.z);
posView[3] = float4(0, 0, 0, 1);
vector upvec = UNITY_MATRIX_IT_MV[1];
vector viewDir = UNITY_MATRIX_IT_MV[2];
vector rorZ = normalize(viewDir);
vector rorX = -normalize(vector(cross(upvec, rorZ), 0));
vector rorY = -normalize(vector(cross(rorZ, rorX), 0));
rotView[0] = rorX;
rotView[1] = rorY;
rotView[2] = rorZ;
rotView[3] = float4(0, 0, 0, 1);
viewMatrix = mul(rotView, posView);
pos = mul(unity_ObjectToWorld, v.vertex);
pos = mul(viewMatrix, pos);
pos = mul(UNITY_MATRIX_P, pos);
o.vertex = pos;
return o;
}
fixed4 frag(v2f i) : SV_Target
{
return fixed4(1, 0, 0, 1);
}
ENDCG
}
}
}
위에서 어렵게 X, Y, Z 기저 벡터를 계산해서 구했지만 결국 처음으로 돌아가서 다음의 코드와 다를 바가 없습니다.
vector rorX = vector(UNITY_MATRIX_V._m00_m01_m02, 0);
vector rorY = vector(UNITY_MATRIX_V._m10_m11_m12, 0);
vector rorZ = vector(UNITY_MATRIX_V._m20_m21_m22, 0);
다음의 글에도 나오지만,
Advanced info on Unity3D's camera matrix
; https://stackoverflow.com/questions/24165915/advanced-info-on-unity3ds-camera-matrix
Model matrix. In scripts: Transform.localToWorldMatrix. In vertex shaders: _Object2World.
View matrix. In scripts: Camera.worldToCameraMatrix. In vertex shaders: UNITY_MATRIX_V.
Projection matrix. In scripts: Camera.projectionMatrix. In vertex shaders: UNITY_MATRIX_P.
UNITY_MATRIX_V나 UNITY_MATRIX_P 행렬은 C# 스크립트에서 Camera.worldToCameraMatrix, Camera.projectionMatrix로 각각 대응한다고 합니다. 따라서 이 값을 shader에 전달해 연산하면 이전의 결과와 동일한 동작을 얻게 됩니다.
실제로 해볼까요? ^^ 다음과 같이 C# 스크립트를 구성하고,
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
[ExecuteInEditMode]
public class SetMatrix : MonoBehaviour {
void Start () {
}
void Update () {
Camera camera = Camera.main;
Shader.SetGlobalMatrix("_viewMatrix", camera.worldToCameraMatrix);
}
}
전달한 _viewMatrix를 이용해 vertex shader를 구성하면,
Shader "Unlit/NewUnlitShader"
{
Properties
{
}
SubShader
{
Tags { "RenderType" = "Opaque" }
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
};
struct v2f
{
float4 vertex : SV_POSITION;
};
float4x4 _viewMatrix;
v2f vert(appdata v)
{
float4 pos;
v2f o;
pos = mul(unity_ObjectToWorld, v.vertex);
pos = mul(_viewMatrix, pos);
pos = mul(UNITY_MATRIX_P, pos);
o.vertex = pos;
return o;
}
fixed4 frag(v2f i) : SV_Target
{
return fixed4(1, 0, 0, 1);
}
ENDCG
}
}
}
Scene 편집 화면에 다음과 같이 출력됩니다.
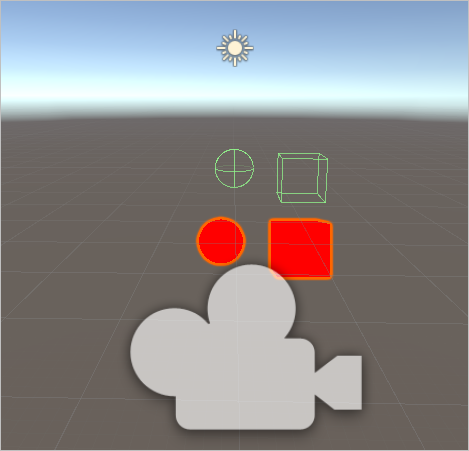
보는 바와 같이 물체의 그려진 위치가 원래 있던 곳에서 (높은 확률로) 벗어나 있습니다. 게다가 Scene 편집 모드 상태에서는 카메라를 돌려도 언제나 같은 자리에 위치하게 됩니다. 이로 인해 자칫 잘못되었다고 생각할 수 있는데요, 아닙니다. ^^ 정상적으로 동작하고 있는 것입니다. 실제로 실행해 Game 뷰로 보면 잘 나오는 것을 확인할 수 있습니다.
Scene 편집 화면에서의 저런 동작은 C# 스크립트가 편집 모드에서 실행될 때 Update 메서드 내에서의 camera.worldToCameraMatrix 값이 순수하게 "Inspector"에 지정된 카메라의 위치로 고정되어 전달하기 때문입니다. 즉, Scene 편집 화면에서도 마우스를 이용해 카메라의 위치와는 전혀 다르게 바라보도록 움직일 수 있는데 그 카메라의 정보를 C# 스크립트에서 사용하지 않고 편집 화면에 떠 있는 카메라 객체의 위치 값만을 고정적으로 사용하기 때문에 저런 현상이 발생하는 것입니다.
그러니까, C# 스크립트에서 shader에 값을 넘겨주는 경우에는 편집 화면을 너무 믿어서는 안 됩니다.
참고로, 다음은 Unity 스크립트에서 main camera에 대한 속성의 출력 예를 보여줍니다.
Main camera
Transform
Position (0, 1, -10)
Rotation (0, 0, 0)
Scale (1, 1, 1)
.aspect 1.353497
.fieldOfView 60
.focalLength 50
.lensShift (0,0)
.nearClipPlane 0.3
.pixelRect (x:0, y:0, width: 716.00, height: 529.00)
.sensorSize (36.0, 24.0)
.cameraToWorldMatrix ( == worldToCameraMatrix.inverse)
1 0 0 0
0 1 0 1
0 0 -1 -10
0 0 0 1
.transpose
1 0 0 0
0 1 0 0
0 0 -1 0
0 1 -10 1
.rotation
(0, 0, 0, 1);
.cullingMatrix
1.279686 0 0 0
0 1.732051 0 -1.732051
0 0 1.0006 9.405821
0 0 1 10
.transpose
1.279686 0 0 0
0 1.732051 0 0
0 0 1.0006 1
0 -1.732051 9.405821 10
.rotation
(0, 0, 0, 1);
.projectionMatrix
1.279686 0 0 0
0 1.732051 0 0
0 0 -1.0006 -0.60018
0 0 -1 0
.transpose
1.279686 0 0 0
0 1.732051 0 0
0 0 -1.0006 -1
0 0 -0.60018 0
.rotation
(0, 0, 0, 1);
.worldToCameraMatrix ( == cameraToWorldMatrix.inverse)
1 0 0 0
0 1 0 -1
0 0 -1 -10
0 0 0 1
Scene 화면의 카메라 객체를 움직이지 않는 한 저 값은 C# 스크립트에서 편집 상태의 shader에 언제나 그대로 넘어가게 됩니다. 반면, _WorldSpaceCameraPos 내장 변숫값은 shader에 Scene 화면의 사용자 조작에 따른 카메라 값을 반영하고 있는 것입니다.
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]