C# - 웨이트 벡터 갱신식을 이용한 퍼셉트론 분류
아래의 책에 보면,
기초 수학으로 이해하는 머신러닝 알고리즘
; https://wikibook.co.kr/math-for-ml/
간단한 선형 분류를 하는 용도의 Perceptron을 설명하는데, 웨이트 벡터 갱신식을 이용해 풀어가는 과정을 그림과 함께 잘 설명해 주고 있어 직관적인 이해를 할 수 있습니다. 이와 함께 그 구현 코드를 다음의 파이썬으로 공개하고 있는데,
math-for-ml / classification1_perceptron.py
; https://github.com/wikibook/math-for-ml/blob/master/classification1_perceptron.py
그럼, C#으로 번역해볼까요? ^^
우선
파이썬 예제에 나온 images1.csv 파일을,
x1,x2,y
153,432,-1
220,262,-1
118,214,-1
474,384,1
485,411,1
233,430,-1
396,321,1
484,349,1
429,259,1
286,220,1
399,433,-1
403,300,1
252,34,1
497,372,1
379,416,-1
76,163,-1
263,112,1
26,193,-1
61,473,-1
420,253,1
시각화하면 다음과 같이 2개의 부류로 나뉘고,
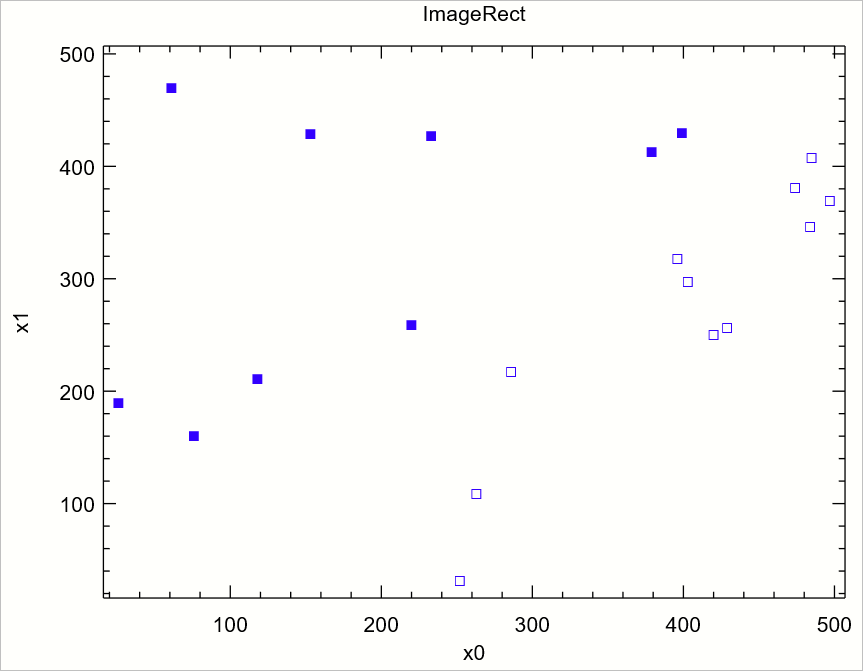
label에 해당하는 y 칼럼의 값이 1인 경우 속이 빈 사각형으로, -1인 경우에는 속이 찬 사각형으로 보입니다. 일단 여기까지만 C# 코드로 작성하면 다음과 같습니다.
static void Main(string[] args)
{
MLContext ctx = new MLContext();
IDataView data = ctx.Data.LoadFromTextFile<ImageRect>("images1.csv", separatorChar: ',', hasHeader: true);
var imgList = ctx.Data.CreateEnumerable<ImageRect>(data, false);
(double x0Min, double x0Max, double x1Min, double x1Max) = imgList.MinMax();
DrawPlotChart(x0Min - 10, x0Max + 10, x1Min - 10, x1Max + 10, (pl) =>
{
pl.lab("x0", "x1", "ImageRect");
pl.col0(PLplot.Color.Blue);
foreach (var item in imgList)
{
pl.poin(item, (item.Y == 1) ? Symbol.Box : Symbol.FilledBox);
}
});
}
private static void DrawPlotChart(double x0Min, double x0Max, double x1Min, double x1Max, Action<PLStream> drawFunc)
{
string chartFileName = "imagerect.svg";
using (var pl = new PLStream())
{
pl.sdev("svg");
pl.sfnam(chartFileName);
pl.spal0("cmap0_alternate.pal");
pl.init();
pl.env(x0Min, x0Max, x1Min, x1Max, AxesScale.Independent, AxisBox.BoxTicksLabelsAxes);
pl.spal0("");
drawFunc(pl);
pl.eop();
pl.gver(out var verText);
}
}
이것을 분류하기 위해 퍼셉트론을 사용할 텐데요. 간단하게 퍼셉트론의 연산을 정리해 보면 그 특성이,
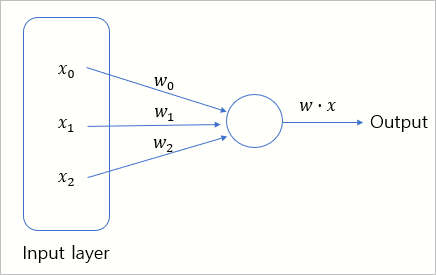
벡터의 내적과 같습니다. 실제로 입력값 x와 가중치 w의 연산 과정이,
fw(x) = (w0 * x0) + (w1 * x1) + (w2 * x2)
= w * x
w, x를 벡터로 본 내적 연산과 동일합니다. 그런데 내적 연산이 어떻게 분류의 기능을 할 수 있는지에 대해서는
책에서 그림과 함께 친절하게, 어렵지 않게 설명하고 있으니 참고를 하시고 여기서는 C# 코드로의 계산 과정을 보겠습니다.
자, 그럼 분류를 하기 위한 (활성함수라고도 불리는) 식별 함수를 다음과 같이 코드로 표현할 수 있고,
// C#
Func<Vector<double>, Vector<double>, int> f = (w, x) => w * x >= 0 ? 1 : -1;
가중치 w 벡터를 images1.csv 파일의 입력값과 label에 따라 학습시키는 갱신식도 코드로 표현한 다음,
// C#
Func<Vector<double>, Vector<double>, double, Vector<double>> updateF = (w, x, y) =>
f(w, x) != y ? w + (y * x) : w;
다음과 같이 5회 반복과 그 출력 결과를 확인할 수 있습니다.
Func<Vector<double>, Vector<double>, int> f = (w, x) => w * x >= 0 ? 1 : -1;
Func<Vector<double>, Vector<double>, double, Vector<double>> updateF = (w, x, y) => f(w, x) != y ? w + (y * x) : w;
Vector<double> weight = Vector<double>.Build.Dense(SystemRandomSource.Default.NextDoubles(2));
Console.WriteLine($"[{0,2:#0}]: w = {weight[0]},{weight[1]}");
for (int i = 0; i < 5; i ++)
{
foreach (var item in imgList)
{
Vector<double> x = item.AsVectorX();
weight = updateF(weight, x, item.Y);
}
Console.WriteLine($"[{i + 1,2:#0}]: w = {weight[0]},{weight[1]}");
}
[ 0]: w = 0.285028267318862,0.885289029630501
[ 1]: w = 372.285028267319,-593.11471097037
[ 2]: w = 613.285028267319,-639.11471097037
[ 3]: w = 613.285028267319,-639.11471097037
[ 4]: w = 613.285028267319,-639.11471097037
[ 5]: w = 613.285028267319,-639.11471097037
5회까지 갈 것도 없이 사실상 2회부터 값의 변동이 없습니다. Weight 벡터가 정해졌으니 이제 그것의 법선을 직선으로 표시해 보면,
IEnumerable<double> x1 = Utils.RangeInclusive(0.0, x0Max, 1.0);
IEnumerable<double> x2 = x1.ForEach((elem) => (-weight[0] / weight[1]) * elem);
DrawPlotChart(x0Min - 10, x0Max + 10, x1Min - 10, x1Max + 10, (pl) =>
{
// ...[생략]...
pl.lsty(LineStyle.ShortDashesShortGaps);
pl.line(x1.ToArray(), x2.ToArray());
});
잘 동작했음을 확인할 수 있습니다.
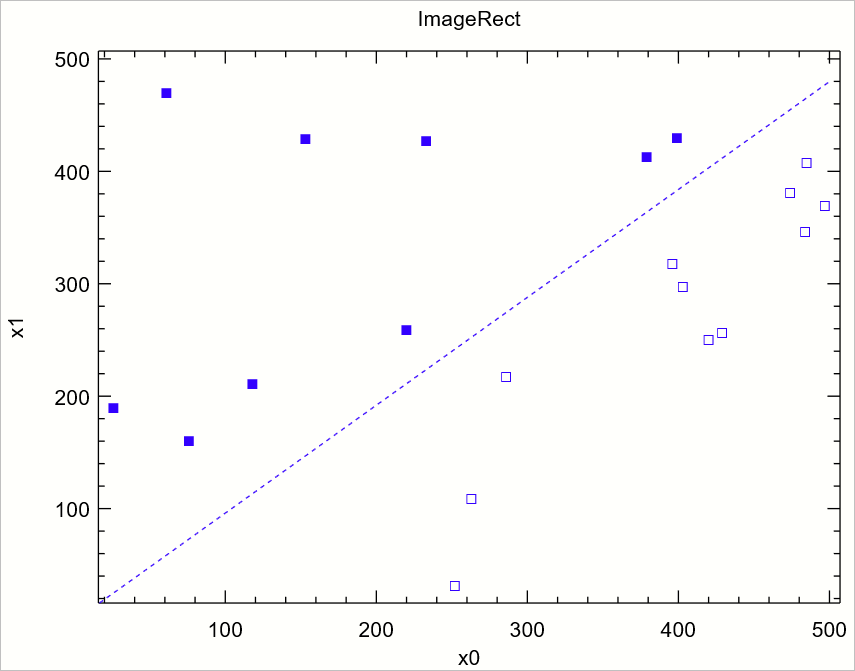
그런데 웹 검색을 해보면 책에서 사용한 갱신식과,
약간 다른 것을 볼 수 있습니다.
wi = wi + η(y - fw(xi)) * xi
하지만 자세히 보면 위의 2개 식은 같습니다. 실제로 label에 해당하는 y 값과 그것의 활성함수가 1과 -1을 반환한다는 점으로 인해 책에서 2개의 경우로 나눈 갱신식을 하나로 합칠 수 있기 때문입니다. 즉, y == f(x)가 같은 경우라면 어차피 y - f(x)는 0이 된다는 점과, 다른 경우라면 y - f(x)가 2 또는 -2가 되기 때문에 책의 갱신식을 다음과 같이 하나로 합칠 수 있습니다.
wi = wi + 0.5 * (y - fw(xi)) * xi
따라서 C# 코드도 기존의 updateF 함수를 다음과 같이 고쳐 쓸 수 있습니다.
// 기존
Func<Vector<double>, Vector<double>, double, Vector<double>> updateF = (w, x, y) =>
(f(w, x) != y) ? w + (y * x) : w;
// 신규
Func<Vector<double>, Vector<double>, double, Vector<double>> updateF = (w, x, y) =>
w + 0.5 * (y - f(w, x)) * x;
여기서 지난 글에 설명한 최소 자승법의 갱신식을 떠 올려보면,
C# - 해석학적 방법을 이용한 최소 자승법
; https://www.sysnet.pe.kr/2/0/11924
위의 갱신식을 "확률 경사 하강법"으로 바꾸고,
마이너스 부호를 식 안으로 넣어 정리해 주면,
웨이트 벡터 갱신식과 구조가 같아집니다. 재미있는 점은, 최소 자승법의 경우 목적함수가 연속이므로 미분한 결과로 나온 수식이었던 반면, 웨이트 벡터 갱신식의 경우에는 활성 함수가 연속적이지 않아 미분으로 나온 것은 아니라는 점입니다. 즉, 활성함수를 설계한 수학자가 label의 값을 -1과 1로 맞춰줌으로써 (아마도 의도했겠지만) 여타 다른 갱신식과 유사한 수식으로 나타낼 수 있게 된 것입니다.
웹 검색을 해보면,
[3편] 파이썬으로 단순 인공신경망인 퍼셉트론 구현하기
; http://sams.epaiai.com/220951769938
퍼셉트론으로 AND, OR 연산을 학습시키는 것이 나옵니다. 그런데 (
책에서 참고한) 우리가 만든 C# 코드로는 AND, OR 학습이 안 됩니다. 예를 들어 AND 데이터로,
x1,x2,y
0,0,-1
0,1,-1
1,0,-1
1,1,1
weight를 학습시킨,
[ 0]: w = 0.488790991012375, 0.944808860749383, 0.633428586010555
[ 1]: w = -0.511209008987625, 1.94480886074938, 0.633428586010555
[ 2]: w = -1.51120900898762, 1.94480886074938, 0.633428586010555
[ 3]: w = -1.51120900898762, 1.94480886074938, 1.63342858601056
[ 4]: w = -2.51120900898762, 1.94480886074938, 0.633428586010555
...
...
가중치를 확인해 보면 다음과 같이 잘못된 결과를 보게 됩니다.
Console.WriteLine(f(AsVector(0, 0), weight)); // -1 (0 AND 0)
Console.WriteLine(f(AsVector(0, 1), weight)); // 1 (0 AND 1)
Console.WriteLine(f(AsVector(1, 0), weight)); // 1 (1 AND 0)
Console.WriteLine(f(AsVector(1, 1), weight)); // 1 (1 AND 1)
"
[3편] 파이썬으로 단순 인공신경망인 퍼셉트론 구현하기" 글을 보면 bias 값이 하나 더 추가되는 것을 볼 수 있는데요. 따라서 우리도 그에 대한 보정을 해주면 정상적으로 출력이 나옵니다.
-1
-1
-1
1
다음은 이것을 반영한 최종 소스 코드입니다.
static void Main(string[] args)
{
MLContext ctx = new MLContext();
IDataView data = ctx.Data.LoadFromTextFile<ImageRect>("bit_and.csv", separatorChar: ',', hasHeader: true);
var imgList = ctx.Data.CreateEnumerable<ImageRect>(data, false);
Func<Vector<double>, Vector<double>, int> f = (w, x) => ((w * x) > 0) ? 1 : -1;
Func<Vector<double>, Vector<double>, double, Vector<double>> updateF = (w, x, y) => w + 0.5 * (y - f(w, x)) * x;
Vector<double> weight = AsVector(SystemRandomSource.Default.NextDoubles(3));
OutputWeights(0, weight);
bool addBias = true;
for (int i = 1; i < 10; i ++)
{
foreach (var item in imgList)
{
Vector<double> x = item.AsVectorX(addBias);
weight = updateF(weight, x, item.Y);
}
OutputWeights(i, weight);
}
}
/*
public class ImageRect
{
// ...[생략]...
public Vector AsVectorX(bool addBias)
{
return Vector.Build.Dense(new double[] { (addBias) ? 1.0 : 0.0, X0, X1 });
}
}
*/
(
첨부 파일은 이 글의 예제 코드를 포함합니다.)
bias를 넣었음에도, 그리고 여전히 선형적인 문제임에도 정상적인 weight 벡터가 구해지지 않는 경우가 있습니다. 가령 다음의 데이터는 x2의 값이 300 이상인 경우 -1, 미만인 경우 1의 데이터입니다.
x1,x2,y
153,432,-1
220,262,-1
118,214,-1
474,384,1
485,411,1
233,430,-1
396,321,1
484,349,1
429,259,1
286,220,-1
399,433,1
403,300,1
252,34,-1
497,372,1
379,416,1
76,163,-1
263,112,-1
26,193,-1
61,473,-1
420,253,1
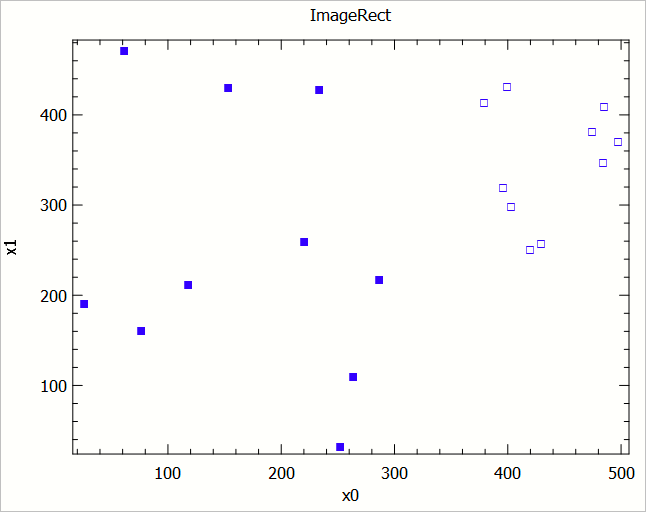
다음과 같이 10회를 학습시켜도 가중치 벡터가 수렴하지 않으며,
[ 0]: w = 0.518085081371518, 0.788236180687433, 0.914021219552504
[ 1]: w = -1.48191491862848, 426.788236180687, 0.914021219552524
[ 2]: w = -3.48191491862848, 532.788236180687, -157.085978780447
[ 3]: w = -6.48191491862848, 521.788236180687, -315.085978780447
[ 4]: w = -9.48191491862848, 443.788236180687, -303.085978780447
[ 5]: w = -12.4819149186285, 480.788236180687, -447.085978780447
[ 6]: w = -13.4819149186285, 498.788236180687, -127.085978780447
[ 7]: w = -16.4819149186285, 487.788236180687, -285.085978780447
[ 8]: w = -19.4819149186285, 409.788236180687, -273.085978780447
[ 9]: w = -22.4819149186285, 446.788236180687, -417.085978780447
x2의 값이 300 이상/미만으로 테스트를 해보면,
Console.WriteLine(f(AsVector(addBias, 100, 250), weight)); // -1 (250이므로 1이어야 함)
Console.WriteLine(f(AsVector(addBias, 200, 350), weight)); // -1
Console.WriteLine(f(AsVector(addBias, 300, 450), weight)); // -1
Console.WriteLine(f(AsVector(addBias, 400, 100), weight)); // 1
잘못된 값이 나오는 것을 볼 수 있습니다. 이 외에도 잘 아시겠지만 XOR 같은 비선형 문제는 당연히 단일 퍼셉트론으로는 학습시킬 수 없습니다.
참고로, "
[3편] 파이썬으로 단순 인공신경망인 퍼셉트론 구현하기" 글에 실린 파이썬 코드에 대해,
import numpy as np
class Perceptron():
def __init__(self, thresholds = 0.0, eta = 0.01, n_iter = 10):
self.thresholds = thresholds
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
self.w_ = np.zeros(1 + X.shape[1])
self.errors_ = []
for _ in range(self.n_iter):
errors = 0
for xi, target in zip(X, y):
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
print(self.w_)
return self
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
return np.where(self.net_input(X) > self.thresholds, 1, -1)
if __name__ == '__main__':
train = np.loadtxt('./data/image300hor.csv', delimiter = ',', skiprows = 1)
X = train[:,0:2]
y = train[:,2]
ppn = Perceptron(eta = 0.1)
ppn.fit(X, y)
print(ppn.errors_)
X = np.array([[0, 250], [0, 350], [1, 450], [1, 100]])
y = np.array([-1, -1, -1, 1])
print(ppn.predict(X))
우리가 만든 C# 코드를 동일하게 출력을 맞춰주고 싶다면 다음의 인자들을 조정해야 합니다.
Func<Vector<double>, Vector<double>, int> f = (w, x) => ((w * x) > 0) ? 1 : -1;
Func<Vector<double>, Vector<double>, double, Vector<double>> updateF = (w, x, y) => w + 0.1 * (y - f(w, x)) * x;
Vector weight = AsVector(0.0, 0.0, 0.0);
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]