C# - 피보나치 수열의 사각형과 황금 나선(Golden spiral) 그리기
지난번 펜타그램에 이어서. ^^
C# - 펜타그램(Pentagram) 그리기
; https://www.sysnet.pe.kr/2/0/1310
피보나치 수의 재미있는 특성 하나를 기하학으로 살펴보겠습니다.
인접한 피보나치 수들의 곱을 홀수 번 더하면 마지막 피보나치 수의 제곱과 같다.
수식으로 표현하면 다음과 같은데요.
1 * 1 + 1 * 2 + 2 * 3 == 9, 마지막 수(3)의 제곱
1 * 1 + 1 * 2 + 2 * 3 + 3 * 5 + 5 * 8 + 8 * 13 + 13 * 21 == 441, 마지막 수(21)의 제곱
1 * 1 + 1 * 2 + 2 * 3 + 3 * 5 + 5 * 8 + 8 * 13 + 13 * 21 + 21 * 34 + 34 * 55 + 55 * 89 + 89 * 144 == 144 * 144
위의 특성을 그림으로 표현하기 위해 피보나치 수열을 구하고,
public class Fibonacci
{
int first = 0;
int second = 1;
public IEnumerable<int> GetNext()
{
while (true)
{
int result = first + second;
first = second;
second = result;
yield return result;
}
}
}
이를 기반으로 각각 Width, Height 값으로 사각형 크기를 구성하고,
public class FibonacciSize
{
Size size;
public FibonacciSize()
{
size = new Size();
size.Height = 0;
size.Width = 1;
}
public IEnumerable<Size> GetNext()
{
Fibonacci fib = new Fibonacci();
foreach (var item in fib.GetNext())
{
int temp = size.Width + size.Height;
size.Height = size.Width;
size.Width = temp;
yield return size;
}
}
}
상하좌우로 뻗어나가는 사각형을 그려주면 다음과 같이 홀 수개의 사각형마다 정사각형을 이루는 것을 보게 되고, 정사각형의 크기(n * n = n제곱)를 구하는 값과 같아지게 되는 것입니다.
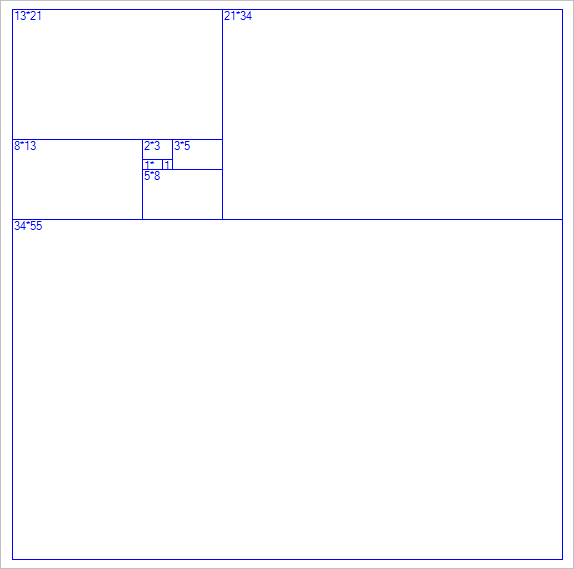
재미 삼아서, 해당 사각형마다 '호'를 그려서 표현하면 다음과 같이 나옵니다.
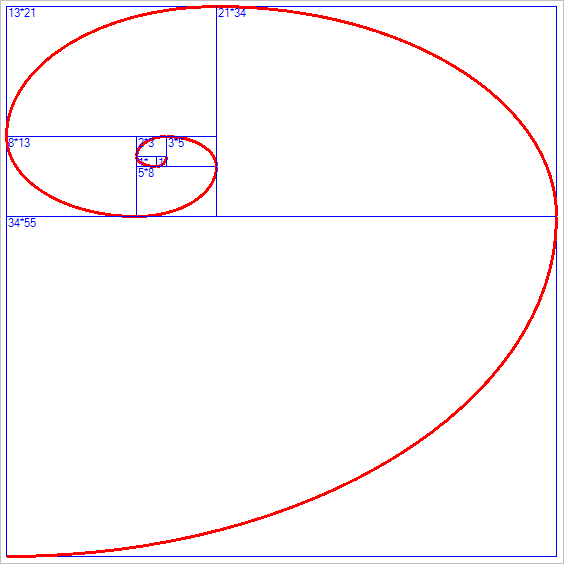
황금나선은, 위의 피보나치 수열을 이용한 사각형과 유사합니다. 단지 정사각형만 피보나치 수열값만큼 증가시켜 주면서 그려나가면 됩니다.
private void DrawGoldenSpiral(Graphics g)
{
SpiralForwrad fd = new SpiralForwrad();
IEnumerator<SpiralDirection> rectForward = fd.GetNext().GetEnumerator();
Fibonacci fib = new Fibonacci();
fib.GetNext();
Rect prev = new Rect();
foreach (var item in fib.GetNext())
{
rectForward.MoveNext();
SpiralDirection sdirection = rectForward.Current;
Rect current = new Rect();
switch (sdirection)
{
case SpiralDirection.Top:
current = new Rect(prev.X, prev.Y - item, item, item);
break;
case SpiralDirection.Left:
current = new Rect(prev.X - item, prev.Y, item, item);
break;
case SpiralDirection.Bottom:
current = new Rect(prev.X, prev.Bottom, item, item);
break;
case SpiralDirection.Right:
current = new Rect(prev.Right, prev.Y, item, item);
break;
}
prev.Plus(current);
Rectangle drawRect = ToCartesian(current);
if (this.ClientRectangle.Contains(drawRect) == false)
{
break;
}
g.DrawRectangle(Pens.Blue, drawRect);
}
}
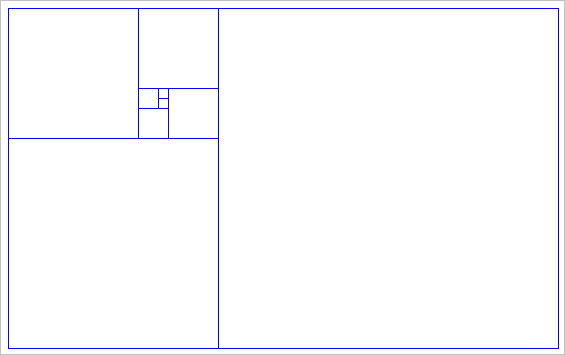
비록 피보나치 수열로 퍼지는 방향으로 사각형을 그리긴 했지만, 모니터의 픽셀 좌표를 무시하고 상상으로 무한히 황금비의 직사각형을 내부에 그려나갈 수 있으므로 결코 다다를 수 없는 '점'으로 수렴하게 되는데요. 이러한 특성을 '클리퍼드 피코버(Clifford Alan Pickover, 1957~)'라는 수학자는 '신의 눈'으로 명칭했다고 합니다.
황금 나선은 이렇게 그려진 정사각형들의 호를 이어서 그려주면 됩니다.
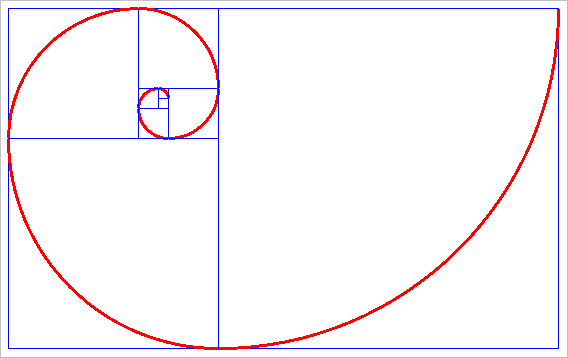 첨부된 소스 코드에는 위의 2가지 코드
첨부된 소스 코드에는 위의 2가지 코드가 들어 있습니다.
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]