단정도/배정도 부동 소수점의 정밀도(Precision)에 따른 형변환 손실
명백히, 아래의 실수 2개는 다른 값입니다.
1129115336.790
1129115376.400
하지만, 이러한 다름은 8바이트 배정도 실수일 때 그런 것이지, 4바이트 단정도 실수일 때는 값이 같습니다.
// C# 11 + .NET 7
static void Main(string[] args)
{
float old = 1129115336.790f;
Console.WriteLine($"{old:F10}");
float current = 1129115376.400f;
Console.WriteLine($"{current:F10}");
}
/* 출력 결과
1129115392.0000000000
1129115392.0000000000
*/
그리고 이건 IEEE 754 부동 소수점 포맷을 따르는 모든 언어에서 같습니다. 에를 들어 Go 언어에서도 동일한 출력을 확인할 수 있습니다.
// Go 1.19.4
func main() {
var old float32 = 1129115336.790
var current float32 = 1129115376.400
fmt.Printf("%.10f\n", old)
fmt.Printf("%.10f\n", current)
}
/* 출력 결과
1129115392.0000000000
1129115392.0000000000
*/
이런 현상이 발생하는 원인은, 배정도 실수의 경우 가수 부분으로 52비트를 할당한 반면, 단정도 실수는 23비트라는 (어쩔 수 없었겠지만) 짧은 정밀도를 가진 탓에 있습니다.
[단정도 실수 - 그림 출처:
https://ko.wikipedia.org/wiki/IEEE_754]

[배정도 실수 - 그림 출처:
https://en.wikipedia.org/wiki/Double-precision_floating-point_format]
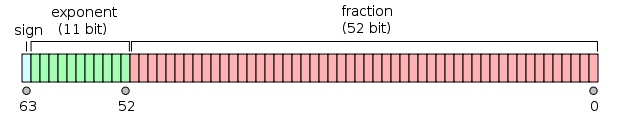
실제로 우리가 테스트했던
10진수 숫자를 2진수로 바꾸면 다음과 같은데요,
// 1129115336.790
0100 0011 0100 1100 1110 1110 1100 1000.1100 1010 0011 1101 0111
// 1129115376.400
0100 0011 0100 1100 1110 1110 1111 0000.0110 0110 0110 0110 0110
앞자리를 1로 놓고 지수를 결정하는 식으로 정규화를 하기 때문에 다음과 같이 23비트에 해당하는 가수가 각각 선택됩니다.
// 1129115336.790
_100 0011 0100 1100 1110 1110 1...
==> 마지막 자리가 1이므로 반올림
_100 0011 0100 1100 1110 1111
// 1129115376.400
_100 0011 0100 1100 1110 1110 1...
==> 마지막 자리가 1이므로 반올림
_100 0011 0100 1100 1110 1111
결국, 정수 영역에 해당하는 것조차 23비트 가수 영역으로는 부족한 상태이므로 소수점 영역은 아예 전부 잘려나갔습니다. 이처럼 float32로 표현되면 그 숫자 값이 1129115376이 되어 값이 같아진 것입니다.
그리고 원래의 값과 비교했을 때, 10진수의 보존된 값은 앞에서 6자리입니다.
위에서 제가 "6자리"의 숫자가 보존되었다고 했는데요, C#의 실수 표현 문서를 보면,
Floating-point numeric types (C# reference)
; https://learn.microsoft.com/en-us/dotnet/csharp/language-reference/builtin-types/floating-point-numeric-types
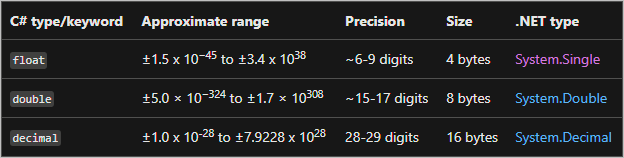
float(32비트)의 경우 Precision이 "~6-9 digits"라는 문구를 볼 수 있는데, 위에서 테스트한 6자리는 그 기준에 부합합니다. 지수를 생각하지 않는다면 가수부의 23비트는 액면 그대로 10진수 7자리에 해당하기 때문에 아마도 일반적인 경우 6~9자리의 10진수 정도에 해당하는 정밀도가 있다고 하는 것 같습니다. (혹시, 정확하게 이때의 정밀도에 대해 설명해 주실 분이 계실까요? ^^ 덧글 부탁드립니다.) 하지만 가수와 지수를 구분해서 보관한다는 실수 표현의 성격상, 가수에 해당하는 비트만 보관할 수 있다면 경우에 따라 전체 숫자 값이 그대로 보존될 수 있는 여지가 있습니다.
가령 위에서 예로 든 "1,129,115,336.790" 값의 정수 부분과 정확히 자릿수가 일치하는 "2,147,483,648" 값은 숫자가 더 큼에도 불구하고 float32로 잘 보존이 됩니다.
float t2 = 2147483648f;
Console.WriteLine($"{t2:F10}"); // 출력 결과: 2147483648.0000000000
왜냐하면 해당 숫자는 2진수로 이렇고,
1000 0000 0000 0000 0000 0000 0000 0000
따라서, 단 1비트만 보관할 수 있어도 나머지는 지수로 감당하므로 숫자가 그대로 보존된 것입니다. 따라서 이런 경우에는 10진수 숫자의 모든 값이 잘 보존되었으므로 정밀도는 10이 된 것입니다.
물론, 23비트만 만족한다면, 더 큰 숫자도 보존할 수 있습니다.
4,784,511,654,127,730,688
==> 0100 0010 0110 0110 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000
가수부에 보존할 값 23비트
.100 0010 0110 0110 0000 0000
실제로 직접 C# 코딩으로 테스트해도 결과가 잘 나옵니다.
BigInteger b = BigInteger.Parse("4784511654127730688");
float t3 = (float)b;
Console.WriteLine($"{t3:F10}");
// 출력 결과: 4784511654127730688.0000000000
저렇게 되면 정밀도는 19가 되는 건가요? ^^
반대로, 10진수로는 0.1인 단순한 값조차도 2진수로는 표현할 수 없다는 한계로 인해 부동 소수에서는 제대로 값을 표현하지 못하는 문제도 있습니다.
// 10진수 0.1
// 2진수 0.0001100110011001100...[1100 반복]....
float f1 = 0.1f;
Console.WriteLine($"{f1:F70}");
double f2 = 0.1;
Console.WriteLine($"{f2:F70}");
/* 출력 결과
0.1000000014901161193847656250000000000000000000000000000000000000000000
0.1000000000000000055511151231257827021181583404541015625000000000000000
*/
이처럼, 가수부와 지수부에 대한 독립적인 역할로 인해 부동 소수점 데이터 타입의 경우에는 (정수와는 달리) 작은 숫자 범위에서는 형변환 손실이 없을 거라는, 또는 그 반대로 큰 숫자 범위에서는 반드시 형변환 손실이 있을 거라는 가정을 해서는 안 됩니다.
암튼, 이런저런 부동 소수점의 특성 때문에 이렇게나 많은 글들을 쓰게 되는군요. ^^
C# - 부동 소수 계산 왜 이렇게 나오죠? (1)
; https://www.sysnet.pe.kr/2/0/10872
C# - 부동 소수 계산 왜 이렇게 나오죠? (2)
; https://www.sysnet.pe.kr/2/0/10873
double 값을 구할 때는 반드시 피연산자를 double로 형변환!
; https://www.sysnet.pe.kr/2/0/11055
C#, C++ - double의 Infinity, NaN 표현 방식
; https://www.sysnet.pe.kr/2/0/11896
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]