GeoGebra 기하 (6) - 대수의 4칙 연산
지오지브라 수학 앱을 이용해,
GeoGebra 기하 - 컴퍼스와 자를 이용한 작도 프로그램
; https://www.sysnet.pe.kr/2/0/11568
그동안 준비해온 내용을 바탕으로 이제 대수의 4칙 연산을 작도할 수 있게 되었습니다. 이를 달리 말하면, 컴퍼스와 자를 이용한 4칙 연산을 할 수 있게 된 것입니다. 예를 들어, 다음과 같이 선분 AB를 a로, 선분 CD를 b로 두고,

다음의 4가지 연산을 자와 컴퍼스 만으로 해보겠습니다.
a + b
a * b
a - b
a / b
1) a + b
더하기 연산자는, AB 선분에 CD 선분을 연결하면 되는데요, 방식은 아래의 글과 같습니다.
GeoGebra 기하 (4) - 선분을 n 배 늘이는 방법
; https://www.sysnet.pe.kr/2/0/11574
단지 다른 것은
Compass를 선분 AB가 아닌 선분 CD의 것을 잰 다음에 점 B에서 원을 그려주면 되는 것입니다. 이렇게!
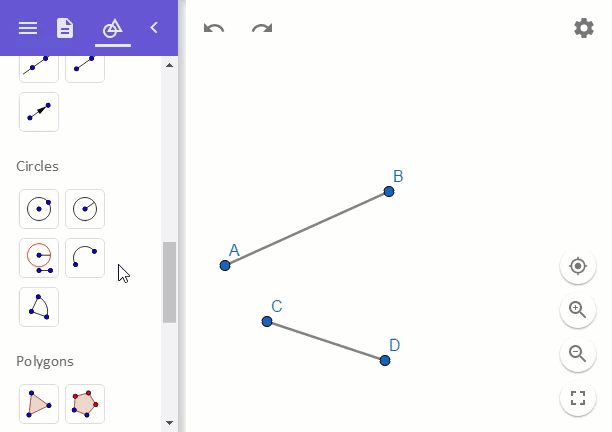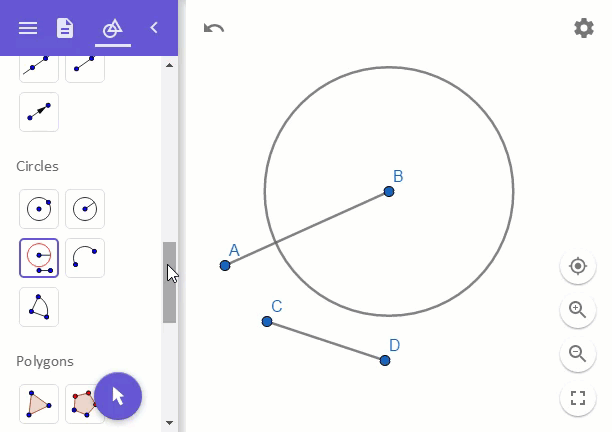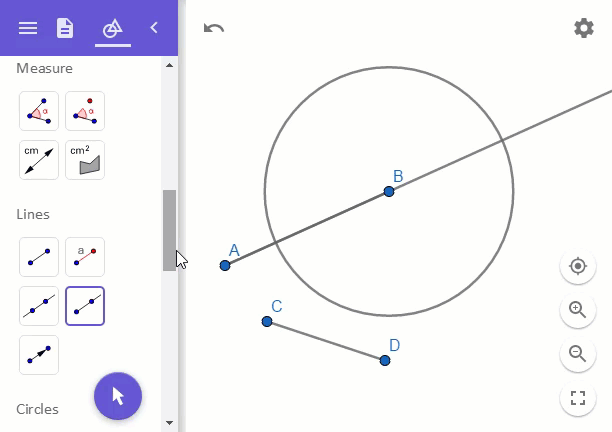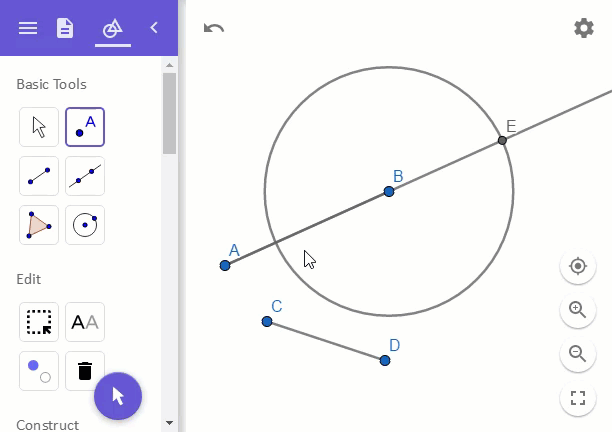
위와 같이 그렸을 때, 선분 AE가 바로 a + b에 해당하는 길이가 됩니다.
2) a - b
빼기 연산도, + 연산자에서 했던 컴퍼스를 이용한 원을 그린 단계까지는 동일합니다. 단지, 점 E의 위치가 점 A와 가까운 곳의 교점에 해당한다는 차이 밖에는 없습니다.
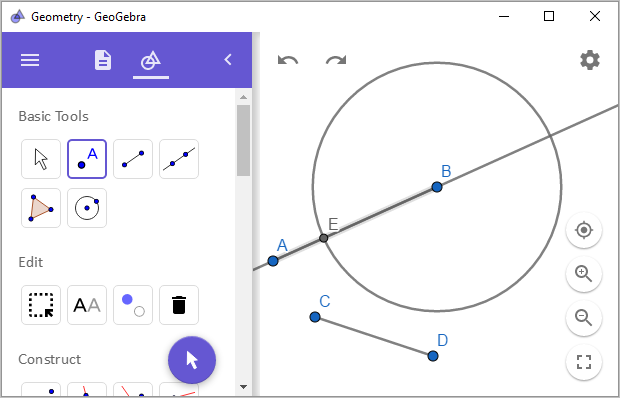
위의 그림에서 선분 AE가 이번에는 "a - b"에 해당하는 길이가 됩니다.
3) a * b
곱하기 연산을 위해
Compass를 이용해 선분 CD에 해당하는 길이로 점 A에서 시작하는 새로운 선을 임의의 방향으로 하나 그어줍니다.
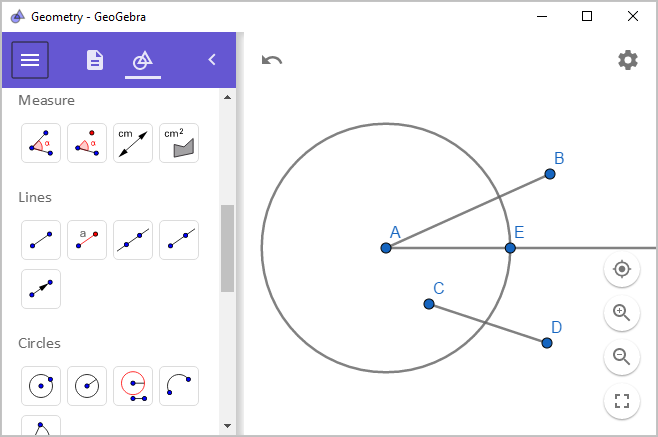
당연히 선분 CD와 선분 AE의 길이는 같습니다. 이제 삼각형의 닮음 조건을 이용해 a * b 연산을 해야 하는데요, 이때 필요한 것이 "단위 길이의 선분"입니다.
작도 가능한 수
; https://ko.wikipedia.org/wiki/%EC%9E%91%EB%8F%84_%EA%B0%80%EB%8A%A5%ED%95%9C_%EC%88%98
고정된 좌표계가 주어진 (혹은 단위 길이의 선분이 주어진) 유클리드 평면 위의 점이 눈금 없는 자와 컴퍼스만을 사용하여 작도할 수 있을 때 그 점을 작도 가능하다고 한다.
이를 위해 "Lines"의 "Segment with Given Length" 도구를 이용해 단위 길이 1에 해당하는 선분을 점 A에서 점 E 방향으로 그려줍니다.
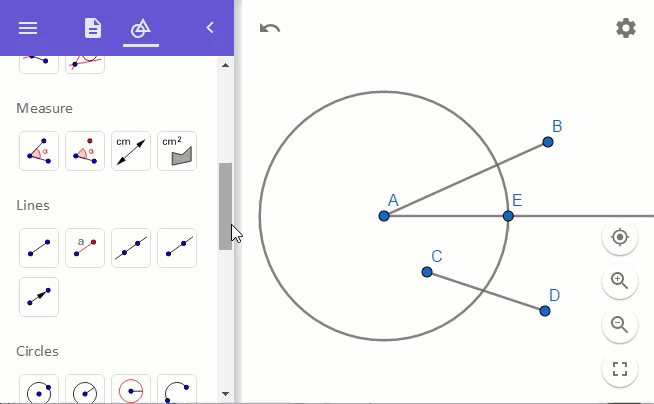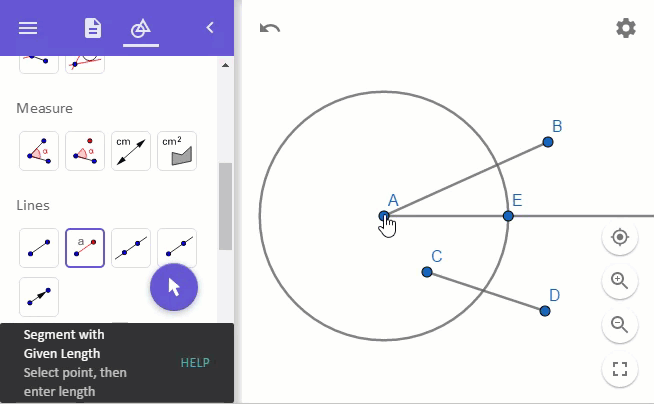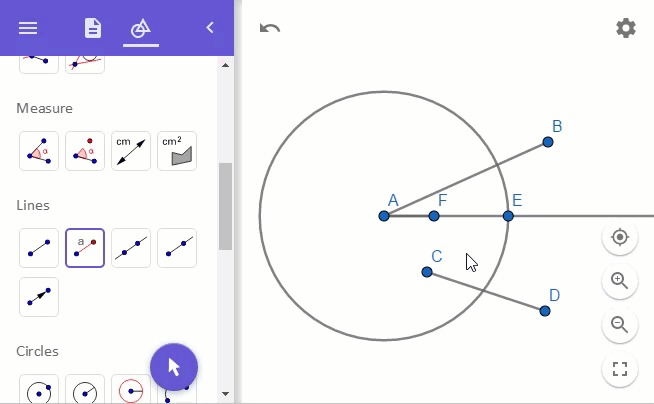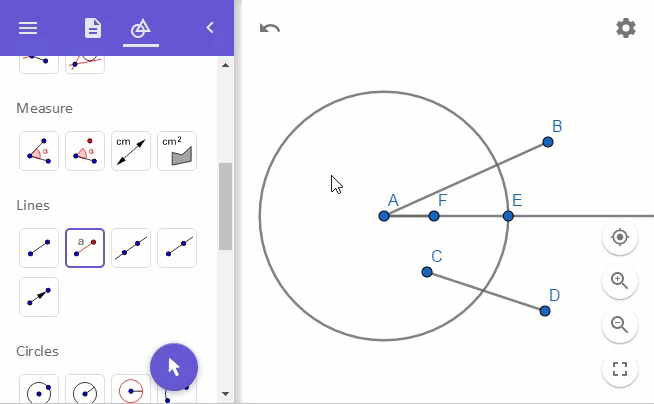
이제 점 F와 점 B를 연결해 줍니다. 그런 다음, 선분 AB를 늘리고 선분 FB와 평행한 선을 점 E로부터 선분 AB에 그립니다.
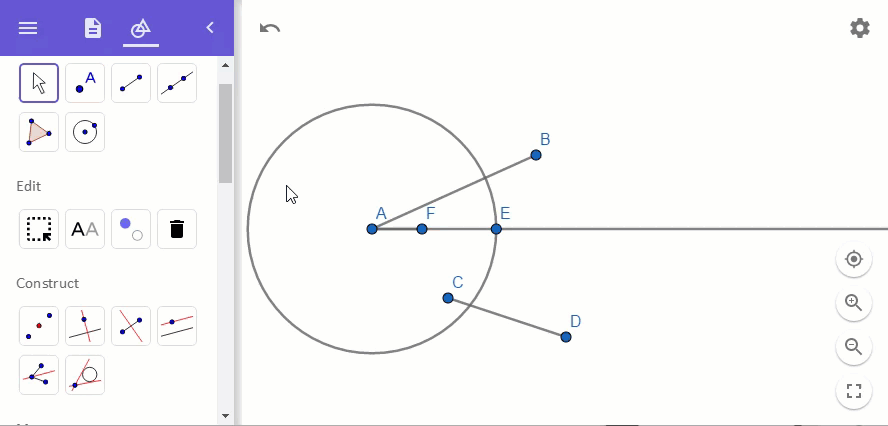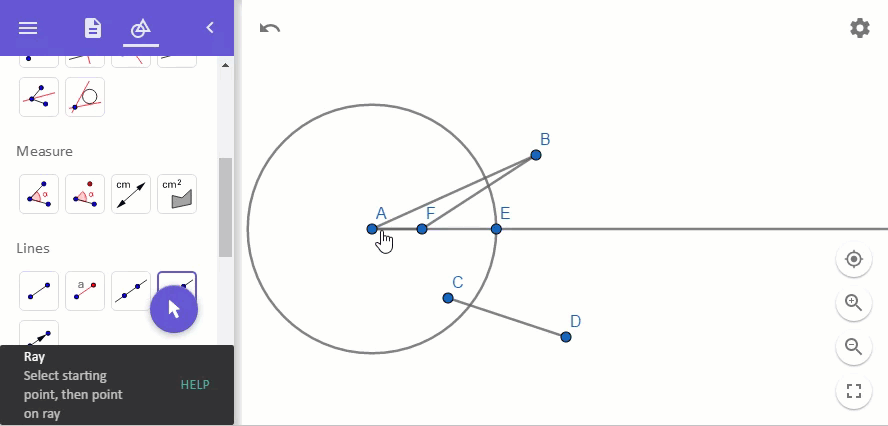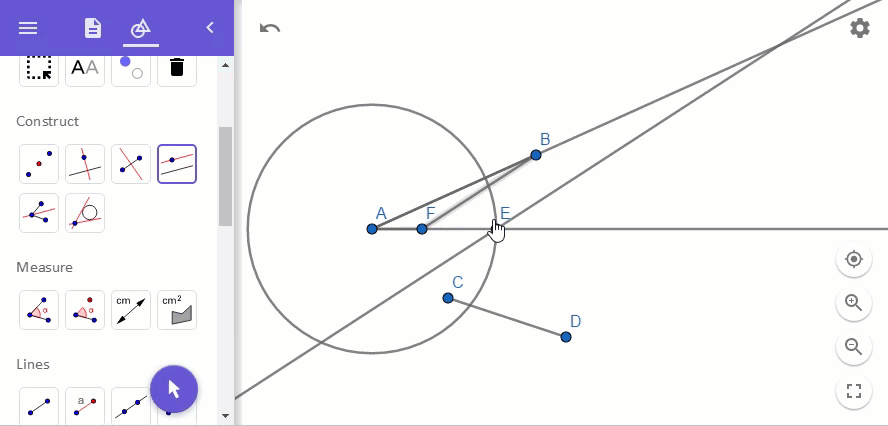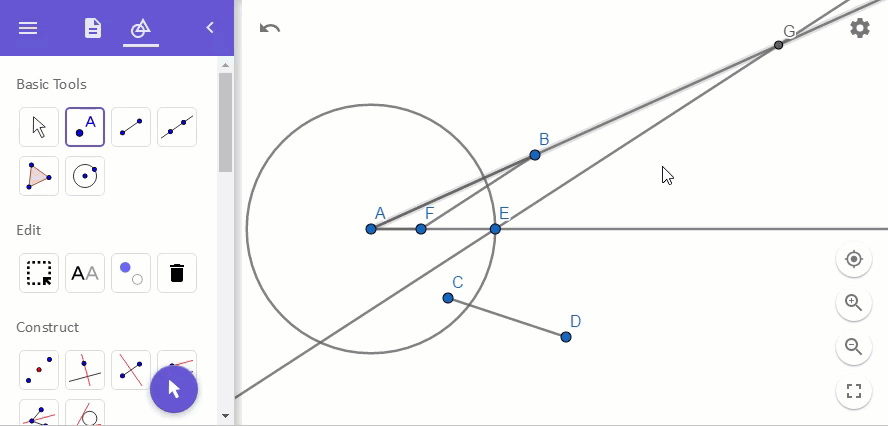
그래서 작도는 다음의 그림과 같이 완성됩니다.
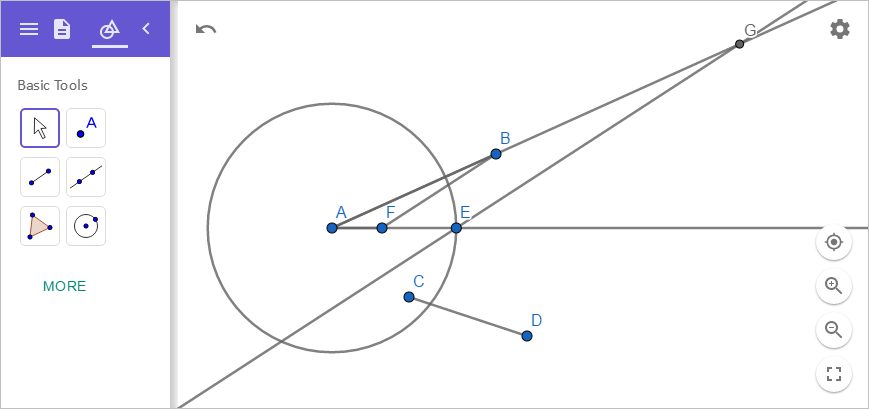
자, 이제 삼각형의 닮음 조건에 의해 다음과 같은 공식이 성립합니다.
선분 AF : 선분 AE = 선분 AB : 선분 AG
==> 1 : 선분 AE = 선분 AB : 선분 AG (선분 AF는 단위 길이이므로)
==> 선분 AE x 선분 AB = 선분 AG
==> 선분 CD x 선분 AB = 선분 AG (선분 AE는 선분 CD를 컴퍼스로 재서 그린 것이므로)
==> a * b = 선분 AG
4) a / b
나누기 역시 곱하기 연산과 유사하게 선분 CD의 길이와 같은 선을 점 A로부터 그린 후, 그 선분 위에 단위 길이를 나타내는 선분 AF를 그리는 단계까지는 같습니다.
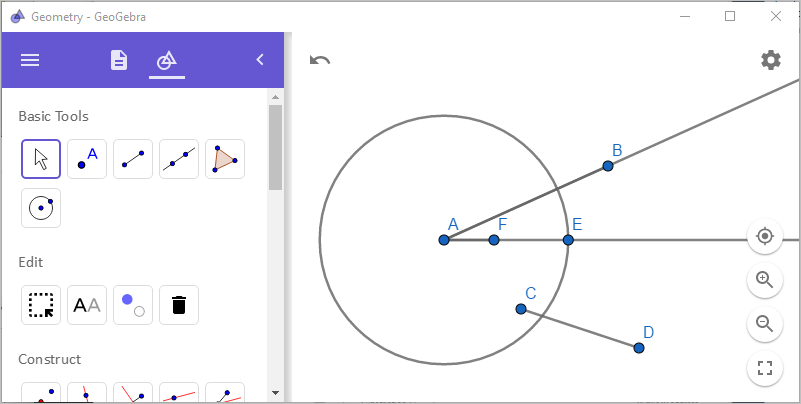
그런데 이번에는 점 E와 점 B를 연결한 선분 BE와 평행한 선을 점 F로부터 그린 후 교점 G를 구합니다.
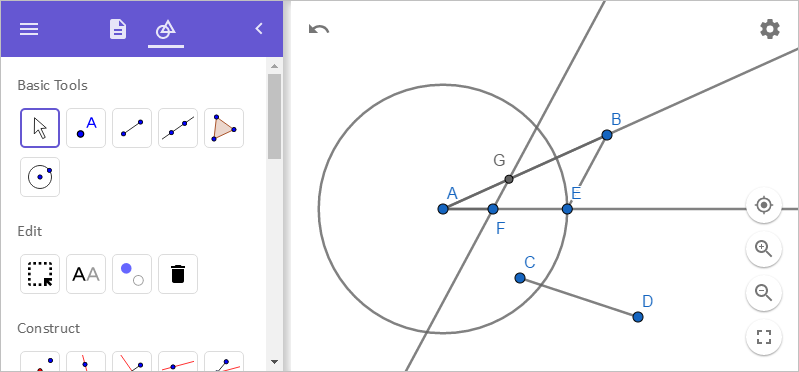
역시 이번에도 삼각형의 닮은 조건을 이용해,
선분 AF : 선분 AE = 선분 AG : 선분 AB
==> 1 : 선분 AE = 선분 AG : 선분 AB (선분 AF는 단위 길이이므로)
==> 선분 AE x 선분 AG = 선분 AB
==> 선분 AG = 선분 AB / 선분 AE
==> 선분 AG = 선분 AB / 선분 CD (선분 AE는 선분 CD를 컴퍼스로 재서 그린 것이므로)
==> 선분 AG = a / b
이것으로 컴퍼스와 자를 이용해 이제 사칙 연산까지 가능해졌습니다.
(
첨부 파일은 위의 작도를 담은 파일입니다.)
Basic Tools
Move
Point
Segment
Circle with Center through Point
Edit
Show / Hide Label
Show / Hide Object
Construct
Midpoint or Center
Perpendicular Line
Perpendicular Bisector
Parallel Line
Measure
Angle
Distance or Length
Lines
Segment
*Segment with Given Length
Ray
Circles
Circle with Center through Point
Compass
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]