C# - 해석학적 방법을 이용한 최소 자승법
다음의 글에 보면,
최소자승법 이해와 다양한 활용예 (Least Square Method)
; https://darkpgmr.tistory.com/56
최소 자승법(최소 제곱법)의 풀이로 대수적 방법과 해석학적 방법이 있다고 하는데요.
대수적 방법은 지난번에 설명했으니, 이번엔 해석학적 방법을 알아보겠습니다. (보다 더 자세한 설명은 "
기초 수학으로 이해하는 머신러닝 알고리즘" 책을 참고하시고 여기서는 간략하게 넘어가겠습니다.)
그러니까, 결국 중요한 것은 데이터를 근사하는 방정식의,
fθ(x) = θ0 + θ1x
매개변수 값(θ
0, θ
1)을 정하는 것입니다. 이를 위해 데이터와의 오차를 계산하는 목적함수에 대해,
각각의 매개변수(θ
0, θ
1)로 편미분한 도함수를 다음과 같이 정리할 수 있습니다.
도함수가 정해졌으니, 이제 목적함수의 최솟값을 구하기 위해 경사하강법을 사용할 수 있고,
C# - 그래프 그리기로 알아보는 경사 하강법의 최소/최댓값 구하기
; https://www.sysnet.pe.kr/2/0/11923
따라서 도함수의 부호에 따라 매개변수를 근사하는 식은 다음과 같이 정리가 됩니다.
끝났군요. ^^ 이제 위의 동작을 코드로 잘 옮겨주면 연산이 진행될수록 θ
0, θ
1 값들은 근사한 1차 방정식의 모습을 갖추게 될 것입니다.
말이 좀 어려운데, 사실 코드로 보면 그다지 어렵지 않습니다. ^^
using MathNet.Numerics.Random;
using Microsoft.ML;
using Microsoft.ML.Data;
using PLplot;
using System;
using System.Collections.Generic;
using System.Linq;
using Microsoft.ML.Data;
class Program
{
static void Main(string[] args)
{
MLContext ctx = new MLContext();
IDataView data = ctx.Data.LoadFromTextFile<ClickData>("click.csv", separatorChar: ',', hasHeader: true);
// 표준화
var xyList = ctx.Data.CreateEnumerable<ClickData>(data, false).NormalizeZscore();
// 매개변수 초기화
double theta0 = SystemRandomSource.Default.NextDouble();
double theta1 = SystemRandomSource.Default.NextDouble();
// 예측 함수
Func<double, double> f = (x) => theta0 + theta1 * x;
// 목적 함수
Func<double, double, double> errorFunc = (x, y) => Math.Pow((y - f(x)), 2);
Func<IEnumerable<ClickData>, double> E = (list) => 0.5 * list.ForEach((e) => errorFunc(e.X, e.Y)).Sum();
// 학습률
double ETA = 1e-03;
// 오차의 차분
double diff = 1.0;
// 갱신 횟수
int count = 0;
// 오차의 차분이 0.01 이하가 될 때까지 매개변수 갱신을 반복
double error = E(xyList);
while (diff > 1e-02)
{
// 갱신 결과를 임시 변수에 저장
double tmp_theta0 = theta0 - ETA * xyList.ForEach((e) => f(e.X) - e.Y).Sum();
double tmp_theta1 = theta1 - ETA * xyList.ForEach((e) => (f(e.X) - e.Y) * e.X).Sum();
// 매개변수 갱신
theta0 = tmp_theta0;
theta1 = tmp_theta1;
// 이전 회의 오차와의 차분을 계산
double currentError = E(xyList);
diff = error - currentError;
error = currentError;
// 로그 출력
count++;
Console.WriteLine($"{count,4:#} 회째: theta0 = {theta0,8:#.0000}, theta1 = {theta1,8:#.0000}, 차분 = {diff,8:#.0000}");
}
// 그래프 출력
double[] xData = xyList.Select((elem) => elem.X).ToArray();
double[] yData = xyList.Select((elem) => elem.Y).ToArray();
DrawPlotChart(xData, yData, f);
}
}
/* 출력 결과
1 회째: theta0 = 9.3955, theta1 = 2.6899, 차분 = 76048.3710
2 회째: theta0 = 17.7905, theta1 = 4.5057, 차분 = 73036.8555
3 회째: theta0 = 26.0177, theta1 = 6.2851, 차분 = 70144.5960
...[생략]...
384 회째: theta0 = 428.9669, theta1 = 93.4392, 차분 = .0145
385 회째: theta0 = 428.9706, theta1 = 93.4400, 차분 = .0139
386 회째: theta0 = 428.9742, theta1 = 93.4407, 차분 = .0133
387 회째: theta0 = 428.9777, theta1 = 93.4415, 차분 = .0128
388 회째: theta0 = 428.9812, theta1 = 93.4422, 차분 = .0123
389 회째: theta0 = 428.9845, theta1 = 93.4430, 차분 = .0118
390 회째: theta0 = 428.9878, theta1 = 93.4437, 차분 = .0113
391 회째: theta0 = 428.9911, theta1 = 93.4444, 차분 = .0109
392 회째: theta0 = 428.9943, theta1 = 93.4451, 차분 = .0105
393 회째: theta0 = 428.9974, theta1 = 93.4458, 차분 = .0101
394 회째: theta0 = 429.0004, theta1 = 93.4464, 차분 = .0097
*/
출력된 그래프를 보면 잘 근사한 것을 확인할 수 있습니다.
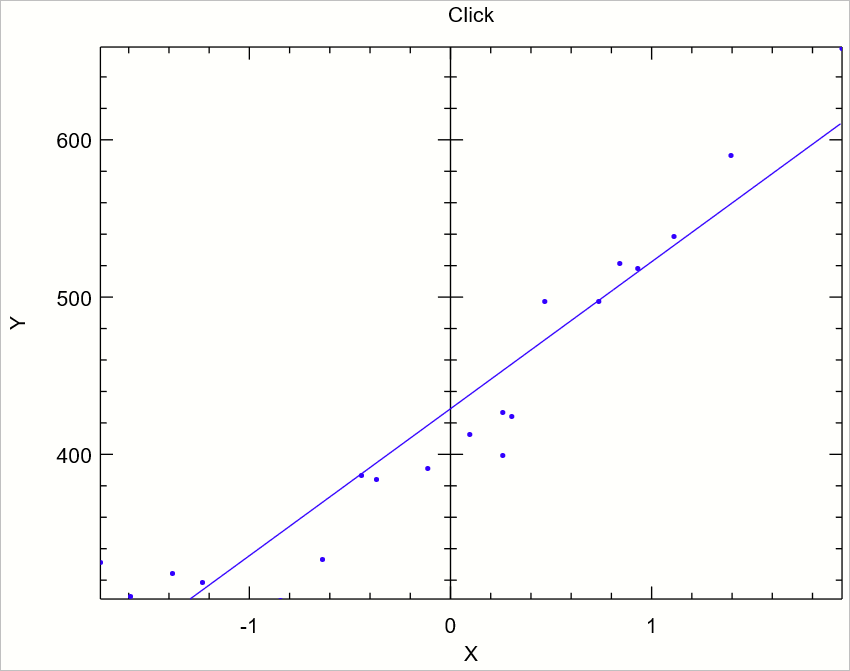
(
첨부 파일은 이 글의 예제 코드를 포함합니다.)
그러니까 위의 소스 코드는 "
기초 수학으로 이해하는 머신러닝 알고리즘" 책의 파이썬 코드를,
math-for-ml / regression1_linear.py
; https://github.com/wikibook/math-for-ml/blob/master/regression1_linear.py
C# 버전으로 변경했다고 보면 되겠습니다. ^^
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]