C# - 최소 자승법의 1차, 2차 수렴 그래프 변화 확인
지난 글에서 최소 자승법(최소 제곱법)을 다뤘고,
C# - 해석학적 방법을 이용한 최소 자승법
; https://www.sysnet.pe.kr/2/0/11924
PLplot을 윈도우 화면으로 출력하는 방법도 배웠으니,
C# - PLplot 출력을 파일이 아닌 Window 화면으로 변경
; https://www.sysnet.pe.kr/2/0/11935
이제 ^^ 최소 자승법이 theta 값을 수정하면서 그래프가 점점 근사해가는 모습을 눈으로 확인할 수 있습니다. ^^
따라서 지난 2개의 글에 실린 예제 코드를 합치면,
private void GraphLSM()
{
MLContext ctx = new MLContext();
IDataView data = ctx.Data.LoadFromTextFile<ClickData>("click.csv", separatorChar: ',', hasHeader: true);
// 표준화
var xyList = ctx.Data.CreateEnumerable<ClickData>(data, false).NormalizeZscore();
// 매개변수 초기화
double theta0 = SystemRandomSource.Default.NextDouble();
double theta1 = SystemRandomSource.Default.NextDouble();
// 예측 함수
Func<double, double> f = (x) => theta0 + theta1 * x;
// 목적 함수
Func<double, double, double> errorFunc = (x, y) => Math.Pow((y - f(x)), 2);
Func<IEnumerable<ClickData>, double> E = (list) => 0.5 * list.ForEach((e) => errorFunc(e.X, e.Y)).Sum();
// 학습률
double ETA = 1e-03;
// 오차의 차분
double diff = 1.0;
// 갱신 횟수
int count = 0;
// 오차의 차분이 0.01 이하가 될 때까지 매개변수 갱신을 반복
double error = E(xyList);
// 그래프를 그리기 위한 데이터 준비
double[] xData = xyList.Select((elem) => elem.X).ToArray();
double[] yData = xyList.Select((elem) => elem.Y).ToArray();
double xMin = xData.Min();
double xMax = xData.Max();
double yMin = yData.Min();
double yMax = yData.Max();
double[] ptX = Utils.RangeInclusive(xMin, xMax, 0.01).ToArray();
double[] ptY = ptY = new double[ptX.Length];
string title = $"{count:#}th: t0 = {theta0:#.00}, t1 = {theta1:#.00}, diff = {diff:#.00}";
this.DoubleBuffered = true;
this.BackgroundImage = DrawPlotChart(xMin - 0.1, xMax + 0.1, yMin - 0.1, yMax + 0.1, title, DrawPlot);
while (diff > 1e-02)
{
Thread.Sleep(100);
// 갱신 결과를 임시 변수에 저장
double tmp_theta0 = theta0 - ETA * xyList.ForEach((e) => f(e.X) - e.Y).Sum();
double tmp_theta1 = theta1 - ETA * xyList.ForEach((e) => (f(e.X) - e.Y) * e.X).Sum();
// 매개변수 갱신
theta0 = tmp_theta0;
theta1 = tmp_theta1;
// 이전 회의 오차와의 차분을 계산
double currentError = E(xyList);
diff = error - currentError;
error = currentError;
count++;
title = $"{count:#}th: t0 = {theta0:#.00}, t1 = {theta1:#.00}, diff = {diff:#.00}";
this.BackgroundImage = DrawPlotChart(xMin - 0.1, xMax + 0.1, yMin - 0.1, yMax + 0.1, title, DrawPlot);
}
void DrawPlot(PLStream pl, string text)
{
pl.lab("x", "y", text);
pl.col0(PLplot.Color.Blue);
for (int i = 0; i < xData.Length; i++)
{
pl.poin(xData[i], yData[i], Symbol.Bullet);
}
pl.lsty(LineStyle.ShortDashesShortGaps);
{
for (int i = 0; i < ptX.Length; i++)
{
ptY[i] = f(ptX[i]);
}
pl.line(ptX, ptY);
}
}
}
실행 시 다음과 같은 애니메이션을 볼 수 있습니다.
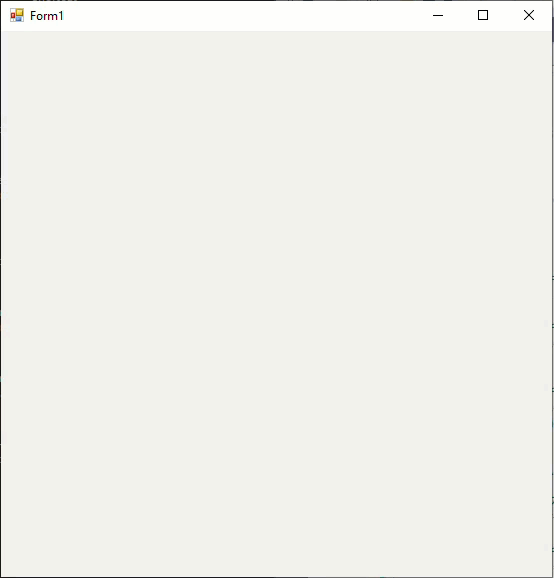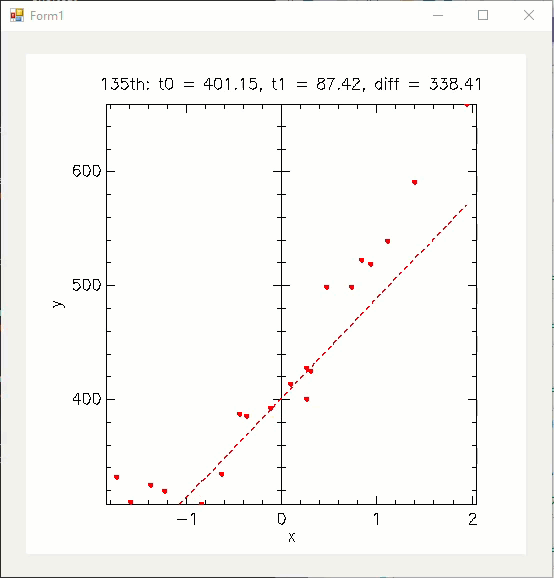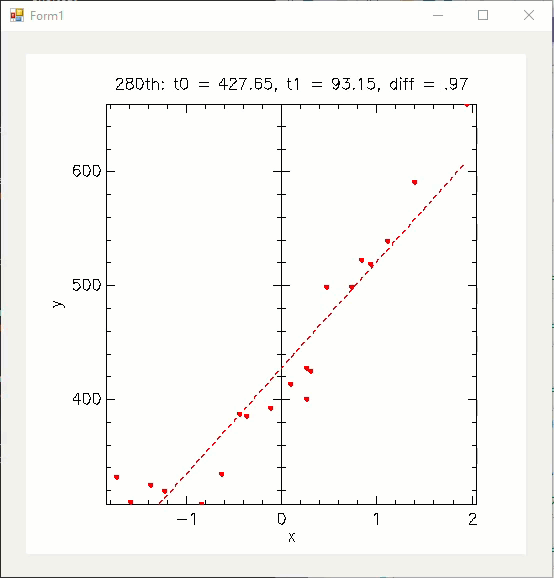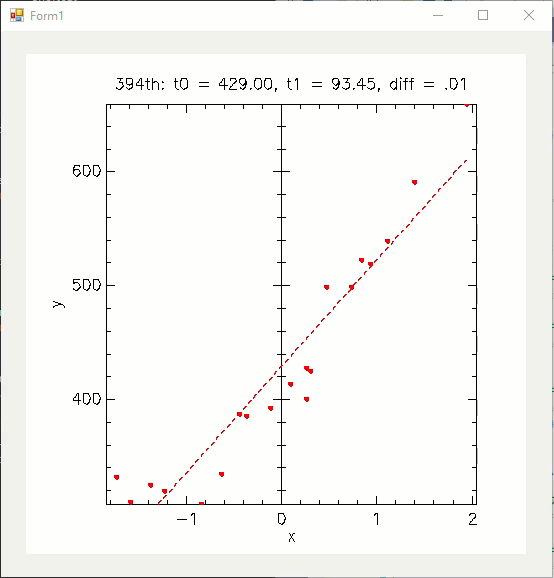
해본 김에, 2차 함수 그래프로 근사하는 장면도 볼 수 있고.
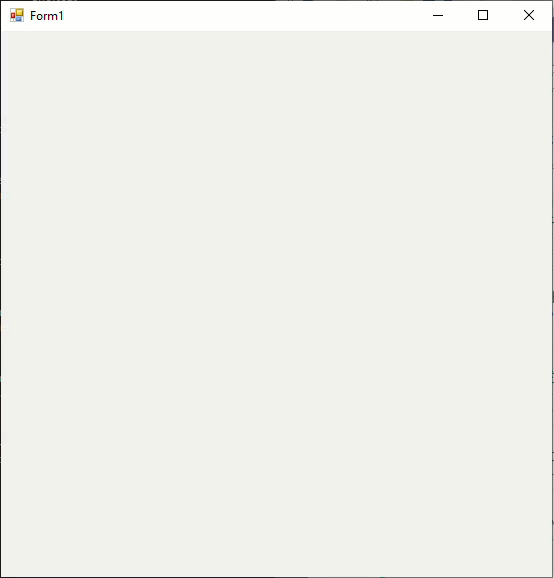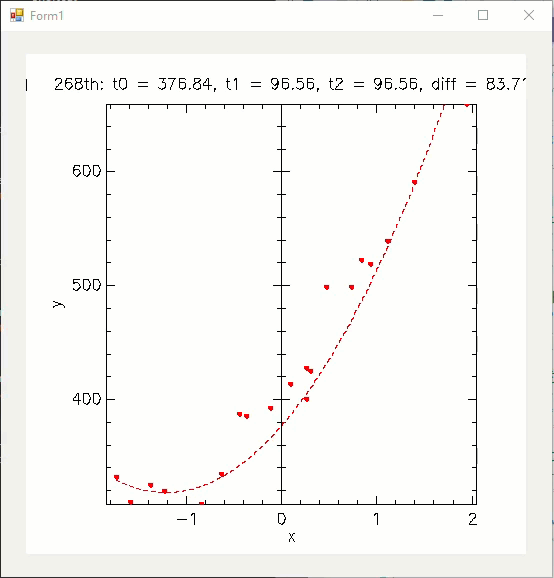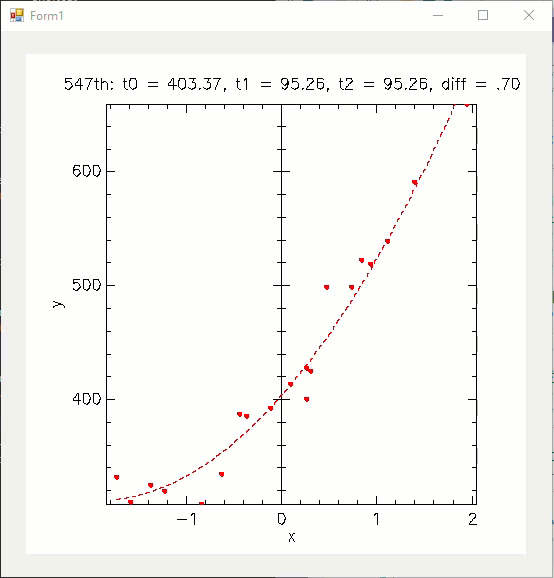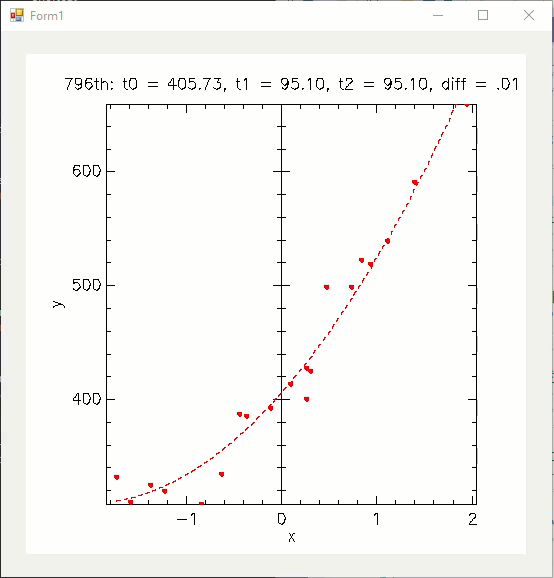
(
첨부 파일은 이 글의 예제 코드를 포함합니다.)
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]