C# - 행렬식을 이용한 최소 자승법(LSM: Least Square Method)
개인적으로 자주 방문하게 되는 사이트가 있는데, 마침 "기초 수학으로 이해하는 머신러닝 알고리즘" 책과 연관된 내용이 나오는군요. ^^
최소자승법 이해와 다양한 활용예 (Least Square Method)
; https://darkpgmr.tistory.com/56
책에서 최소 자승법(최소 제곱법)을 해석학적 방법으로 접근해 행렬식으로 정리하는데, 위의 글을 보면 행렬로 정리한 내용을 더 쉽게 이해할 수 있습니다. 그럼, 실습을 한번 해볼까요? ^^
지난 글에서 설명한 click.csv로 다뤄볼 텐데요,
x,y
235,591
216,539
148,413
35,310
85,308
204,519
49,325
25,332
173,498
191,498
134,392
99,334
117,385
112,387
162,425
272,659
159,400
159,427
59,319
198,522
ML.NET의 라이브러리를 이용하면 다음과 같이 로드해,
using Microsoft.ML.Data;
class ClickData
{
[LoadColumn(0)]
public int X { get; set; }
[LoadColumn(1)]
public int Y { get; set; }
}
class Program
{
static void Main(string[] args)
{
MLContext ctx = new MLContext();
IDataView data = ctx.Data.LoadFromTextFile<ClickData>("click.csv", separatorChar: ',', hasHeader: true);
}
}
Plot 데이터를
지난번과 마찬가지로 그릴 수 있습니다.
var xyList = ctx.Data.CreateEnumerable<ClickData>(data, true);
double[] xData = xyList.Select(xy => (double)xy.X).ToArray();
double[] yData = xyList.Select(xy => (double)xy.Y).ToArray();
DrawPlotChart(xData, yData);
private static void DrawPlotChart(double[] xData, double[] yData)
{
string chartFileName = "click.svg";
int xMin = 0;
int yMin = 0;
int xMax = (int)xData.Max() + 10;
int yMax = (int)yData.Max() + 10;
using (var pl = new PLStream())
{
pl.sdev("svg");
pl.sfnam(chartFileName);
pl.spal0("cmap0_alternate.pal");
pl.init();
pl.env(xMin, xMax, yMin, yMax, AxesScale.Independent, AxisBox.BoxTicksLabelsAxes);
pl.lab("X", "Y", "Click");
char code = Symbol.Bullet; // == 17;
pl.col0(2); //Blue
pl.poin(xData, yData, code);
pl.eop();
pl.gver(out var verText);
}
}
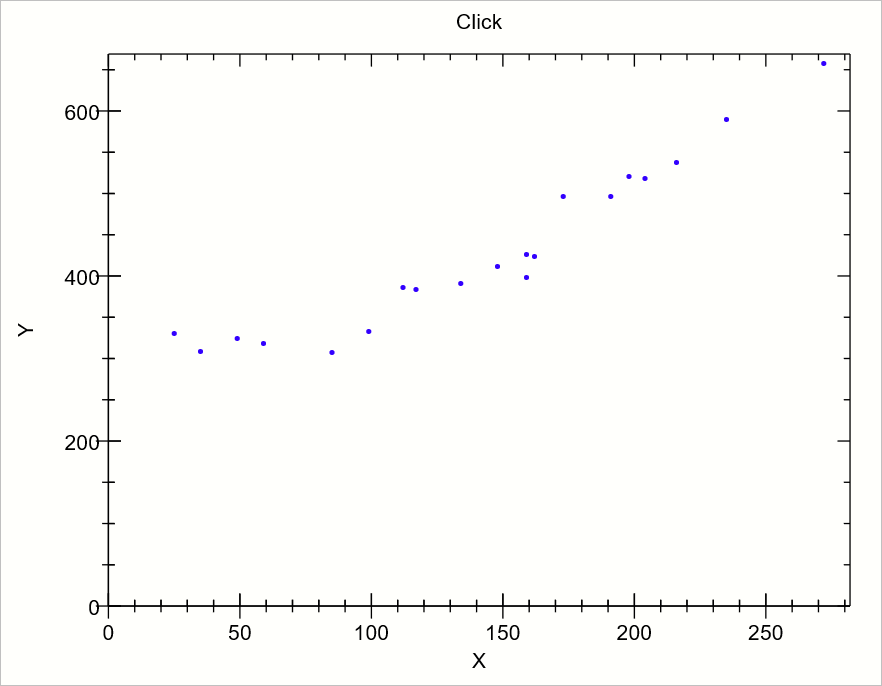
자, 그럼 이제 위의 데이터 분포를 근사시킬 1차 함수를 구해야 하는데요.
θ0 + θ1x1 = y1
θ0 + θ1x2 = y2
...
θ0 + θ1xn = yn
"
최소자승법 이해와 다양한 활용예 (Least Square Method)" 글에서 설명한 데로 이것은 행렬식으로 다룰 수 있고,
방정식의 θ
1, θ
0 요소는 결국 A 행렬의 의사 역행렬을 구해 계산하는 것으로 쉽게 처리할 수 있습니다.
AX=B
A-1AX=A-1B
X=A-1B
다행히 일반적인 역행렬과는 달리 의사 역행렬은,
의사역행렬
; https://ko.wikipedia.org/wiki/%EC%9D%98%EC%82%AC%EC%97%AD%ED%96%89%EB%A0%AC
항상 존재하며, 유일하기 때문에 안전하게 언제나 사용할 수 있습니다. 즉, 근사식에 따른 1차 함수를 언제나 구할 수 있다는 의미입니다. 자, 그럼 이걸 코드로 표현해야겠지요. ^^
우선, A 행렬은 Click 데이터의 X 데이터와 함께 두 번째 칼럼의 값이 1로 채워져 있는 것입니다. 이것을
MathNet의 행렬로 다음과 같이 만들어 줄 수 있습니다.
Matrix<double> matA = CreateMatrix.DenseOfColumnMajor(xData.Count(), 1, xData);
Vector<double> add1 = Vector<double>.Build.DenseOfArray(Enumerable.Repeat(1.0, xData.Count()).ToArray());
Matrix<double> matAwith1 = matA.InsertColumn(1, add1);
/* matAwith1 행렬
235 1
216 1
148 1
35 1
85 1
204 1
49 1
25 1
.. ..
159 1
159 1
59 1
198 1
*/
남은 작업은 의사 역행렬을 구하고 B 행렬과 곱해주면 방정식의 (θ
1, θ
0) 값으로 이뤄진 행렬을 얻게 됩니다.
Matrix<double> matB = CreateMatrix.DenseOfColumnMajor(yData.Count(), 1, yData);
Matrix<double> pinvMatA = matAwith1.PseudoInverse();
Matrix<double> matX = pinvMatA * matB;
double theta1 = mat[1, 1];
double theta0 = mat[1, 0];
/*
matX[0, 0] == θ1
matX[1, 0] == θ0
*/
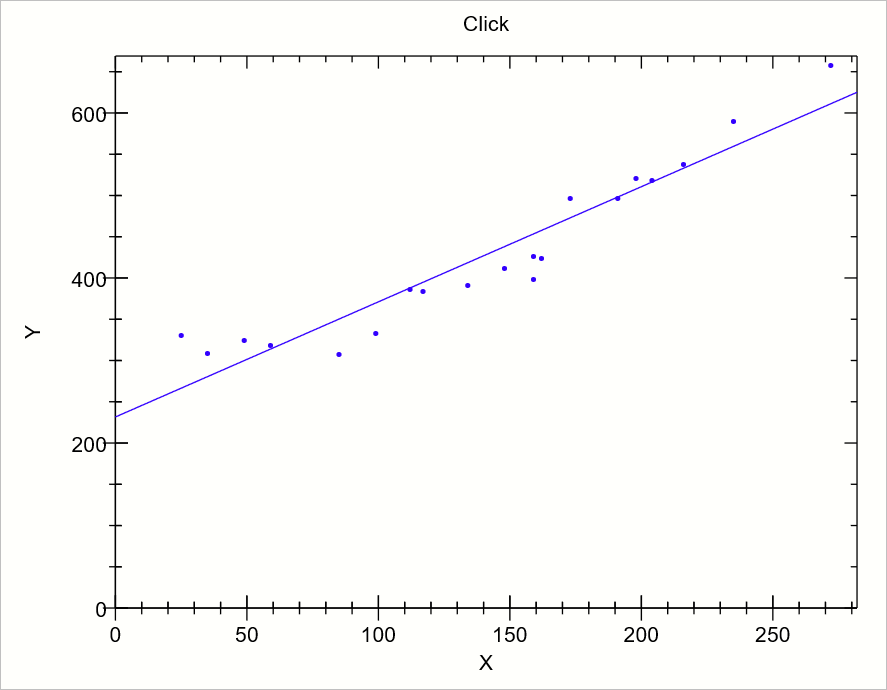
실제로 연산을 해보면 (1.39551018043075, 231.545758451005) 값이 얻어지는데, 따라서 Click 데이터를 근사하는 방정식은 다음과 같이 이뤄집니다.
Console.WriteLine($"y = {theta0} + {theta1} * x");
/* 출력 결과
y = 231.545758451005 + 1.39551018043075 * x
*/
계산 끝났군요. ^^ 이제 이렇게 구한 1차 방정식을 Plot 차트에 추가하면,
Func<double, double> func =
(x) => theta0 + theta1 * x;
double y1 = func(0);
double y2 = func(300);
DrawPlotChart(xData, yData, new double[] { 0, 300 }, new double[] { y1, y2 });
private static void DrawPlotChart(double[] xData, double[] yData, double [] ptX, double [] ptY)
{
...[생략]...
pl.poin(xData, yData, code);
pl.line(ptX, ptY);
...[생략]...
}
다음과 같이 근사하게, 잘 근사한 직선을 볼 수 있습니다. ^^
(
첨부 파일은 이 글의 예제 프로젝트를 포함합니다.)
.NET Core 프로젝트에서 "PLplot" 관련해 다음과 같은 오류가 발생한다면?
Unhandled Exception: System.DllNotFoundException: Unable to load DLL 'plplot' or one of its dependencies: The specified module could not be found. (Exception from HRESULT: 0x8007007E)
at PLplot.Native.mkstrm(Int32& p_strm)
at PLplot.PLStream..ctor() in C:\projects\plplotnet\PLplotNet\PLStream.cs:line 23
at Program.DrawPlotChart(IEnumerable`1 xyList) in F:\ConsoleApp1\ConsoleApp1\Program.cs:line 41
at Program.Main(String[] args) in F:\ConsoleApp1\ConsoleApp1\Program.cs:line 20
이번엔
지난번 상황과 다소 다릅니다. .NET Core 2.1 프로젝트였는데, 로드된 PLplotNet.dll은 다음의 경로였고,
%USERPROFILE%\.nuget\packages\plplot\5.13.7\lib\netstandard2.0\PLplotNet.dll
plplot의 네이티브 모듈들은 정상적으로 "%USERPROFILE%\.nuget\packages\plplot\5.13.7\runtimes\win-x64\native"에 위치하고 있었습니다. 문제의 원인은, .NET Core 2.1 프로젝트의 "Platform"이 "AnyCPU"였다는 것으로 예전에 설명한 적이 있는,
.NET Core 오류 - 0x80131620 Unable to load DLL 'libuv'
; https://www.sysnet.pe.kr/2/0/11389
상황과 동일한 오류입니다. 따라서, "Platform target"을 "AnyCPU"가 아닌 "x64"로 명시적인 설정을 하면 오류가 발생하지 않습니다.
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]