그래프 그리기로 알아보는 뉴턴-랩슨(Newton-Raphson's method)법과 제곱근 구하기 - C#
뉴턴-랩슨법은 방정식의 근사해를 구하는 방법인데요,
뉴턴법/뉴턴-랩슨법의 이해와 활용(Newton's method)
; http://darkpgmr.tistory.com/58
이론이 꽤나 직관적입니다.
간단하게 프로그램을 만들어 가면서 예를 들어볼까요? ^^ 다음의 2차 방정식으로 시작해 보겠습니다.
y = x2 - 10
그래프를 그리기 위해 우선 x, y 기준선을 그려보겠습니다.
using System;
using System.Drawing;
using System.Windows.Forms;
namespace WindowsFormsApplication1
{
public partial class Form1 : Form
{
Point _ptCenter;
public Form1()
{
InitializeComponent();
SetStyle(ControlStyles.ResizeRedraw | ControlStyles.UserPaint | ControlStyles.AllPaintingInWmPaint, true);
UpdateStyles();
}
private void Form1_Load(object sender, EventArgs e)
{
this.Width = 800;
this.Height = 800;
}
protected override void OnPaintBackground(PaintEventArgs e)
{
e.Graphics.Clear(Color.White);
}
protected override void OnPaint(PaintEventArgs e)
{
Graphics g = e.Graphics;
_ptCenter = DrawXYBase(g);
}
private Point DrawXYBase(Graphics g)
{
int centerX = this.Width / 2;
int centerY = this.Height / 2;
g.DrawLine(Pens.Black, 0, centerY, this.Width, centerY);
g.DrawLine(Pens.Black, centerX, 0, centerX, this.Height);
return new Point(centerX, centerY);
}
}
}
우리가 원하는 2차 방정식은 다음과 같이 간단하게 람다식으로 표현할 수 있습니다.
Func<float, float> orgFunc = (x) => (float)(x * x - 10);
x의 증가에 따라 구해지는 y 값에 따라 (x, y) 좌표에 점을 찍어나가는 방법으로 그래프를 표현할 건데요. 아쉽게도 x
2의 큰 차이로 y 값이 크게 증가하기 때문에 x 변위로 그래프를 그리기에는 좀 맞지 않습니다. 따라서 다음의 역함수를 구해,
Func<float, float> inversedF = (y) => (float)Math.Sqrt(y + 10);
거꾸로 y 값을 바꿔가면서 x 좌표를 구할 것입니다. 이 함수를 이용해 그래프를 그리면,
protected override void OnPaint(PaintEventArgs e)
{
Graphics g = e.Graphics;
_ptCenter = DrawXYBase(g);
Func<float, float> orgFunc = (x) => (float)(x * x - 10);
Func<float, float> inversedF = (y) => (float)Math.Sqrt(y + 10);
DrawGraph(inversedF, g);
}
private void DrawGraph(Func<float, float> inversedF, Graphics g)
{
for (float y = -_ptCenter.Y; y < 0; y ++)
{
float x = inversedF(y);
if (float.IsNaN(x) == true)
{
continue;
}
DrawPixel(g, Brushes.Black, x, y);
DrawPixel(g, Brushes.Black, -x, y);
}
for (float y = 0; y < _ptCenter.Y; y ++)
{
float x = inversedF(y);
if (float.IsNaN(x) == true)
{
continue;
}
DrawPixel(g, Brushes.Black, x, y);
DrawPixel(g, Brushes.Black, -x, y);
}
}
private void DrawPixel(Graphics g, Brush brush, float x, float y)
{
PointF pt = Projection(x, y);
g.FillRectangle(brush, pt.X, pt.Y, 1, 1);
}
private PointF Projection(float x, float y)
{
return new PointF(x + _ptCenter.X, -y + _ptCenter.Y);
}
실행 결과가 이렇게 구해집니다.
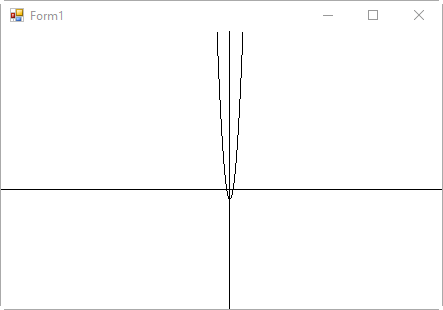
너무 멋이 없군요. ^^; 그래서 좀 더 극적인 효과를 높이기 위해 그래프의 기울기를 완만하게 할 수 있도록 1보다 작은 임의의 값을 곱하겠습니다.
float _slopeForGraph = 70.0f;
Func<float, float> orgFunc = (x) => (float)(1 /_slopeForGraph * x * x - 10);
Func<float, float> inversedF = (y) => (float)Math.Sqrt((y + 10) * _slopeForGraph);
이렇게 하면 좀 더 볼만하게 바뀌는데,
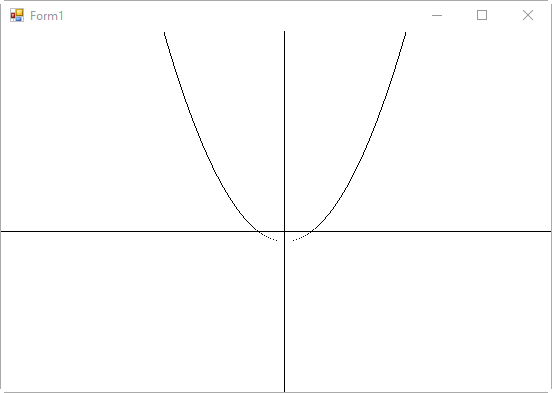
여전히 아쉽게도 하단의 영역이 뚫린 영역이 좀 거슬립니다. 이를 보완하기 위해 y의 증감을 1에서 0.1 정도로 낮춰주면,
float _incOffset = 0.1f;
private float DrawTangentLine(Func<float, float> slopeFunc, Graphics g)
{
float minY = 100;
float minX = 0;
for (float x = -_ptCenter.X; x < 0; x += _incOffset)
{
// ...[생략]...
}
for (float x = 0; x < _ptCenter.X; x += _incOffset)
{
// ...[생략]...
}
return minX;
}
이제야 좀 그래프다운 모습이 나옵니다. ^^
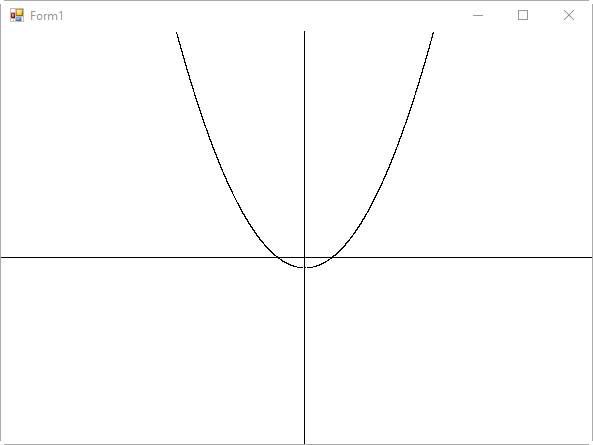
자, 이제 x 좌표의 아무 값이나 (하지만 극적인 효과를 위해 화면에 보일 정도의 값으로) 선택해서 (x * x - 10) 방정식에 대입해 나오는 y 좌표까지의 선을 연결합니다.
protected override void OnPaint(PaintEventArgs e)
{
// ...[생략]...
DrawGraph(inversedF, g);
float startX = 150.0f;
DrawVerticalLine(orgFunc, g, startX);
}
private void DrawVerticalLine(Func<float, float> orgFunc, Graphics g, float x)
{
float y = orgFunc(x);
for (float y1 = 0; y1 < y; y1++)
{
DrawPixel(g, Brushes.Blue, x, y1);
}
}
그럼, 이렇게 나오겠죠?!
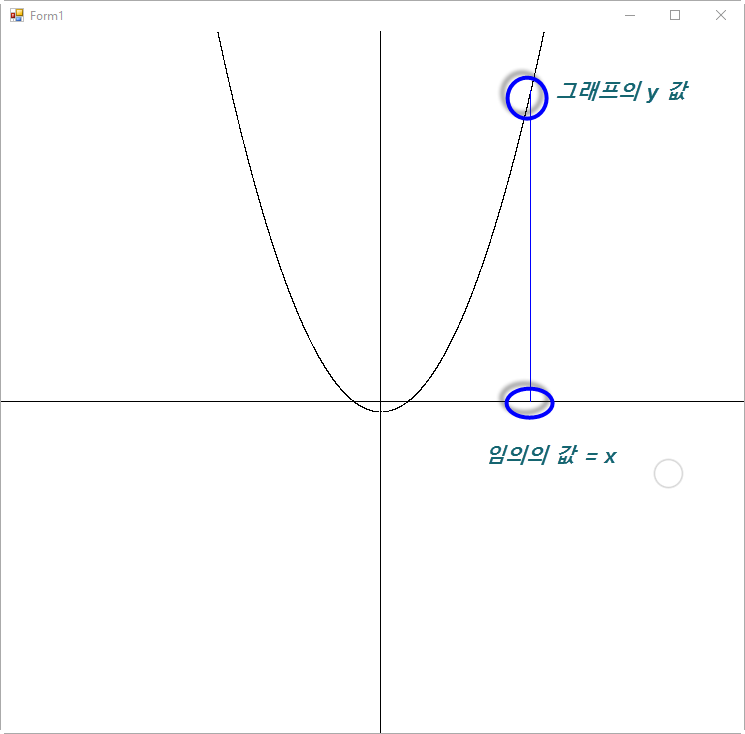
바로 저렇게 수직선과 2차 방정식 그래프가 만난 점의 접선을 구해 그려보겠습니다. 접선은 1차 방정식이므로 다음과 같은 유형으로 나와야 합니다.
y = a * x + b
여기서 접선의 기울기 a 값은 수직선이 만난 2차 방정식 그래프 지점의 기울기와 같습니다. 따라서 원래의 2차 방정식을 미분해 "y = 2 * x" 식을 구할 수 있고 여기에 x 값을 수직선의 x 값으로 대체해 주면 됩니다. 따라서 "y = a * x + b"의 a는 다음의 식으로 구할 수 있습니다.
float startX = 150.0f; // 임의로 정한 x == 150.0f;
float lineSlope = (1 / _slopeForGraph) * 2.0f * startX;
a 값을 구했으니 "y = a * x + b"에서의 b 값을 구해야 하는데요. 역시 2차 방정식에 x를 대입했을 때 나오는 y 값의 (x, y) 쌍이 접선 방정식에서도 그대로 구해져야 한다는 점을 이용해 다음과 같이 구할 수 있습니다.
Func<float, float> orgFunc = (x) => (float)(1 /_slopeForGraph * x * x - 10);
float startX = 150.0f;
float lineSlope = (1 / _slopeForGraph) * 2.0f * startX;
float slopeBParam = (orgFunc(startX) - (lineSlope * startX));
자, 그럼 이제 접선의 방정식을 다음과 같이 구성할 수 있고,
protected override void OnPaint(PaintEventArgs e)
{
// ...[생략]...
Func<float, float> slopeLineFunc = (x) => (lineSlope * x + slopeBParam);
DrawTangentLine(slopeLineFunc, g);
}
void DrawTangentLine(Func<float, float> slopeFunc, Graphics g)
{
for (float x = -_ptCenter.X; x < 0; x += _incOffset)
{
float y = slopeFunc(x);
DrawPixel(g, Brushes.Red, x, y);
}
for (float x = 0; x < _ptCenter.X; x += _incOffset)
{
float y = slopeFunc(x);
DrawPixel(g, Brushes.Red, x, y);
}
}
이를 그려서 나온 직선을 통해 다시 y = 0이 되는 지점의 x 값을 구할 수 있습니다.
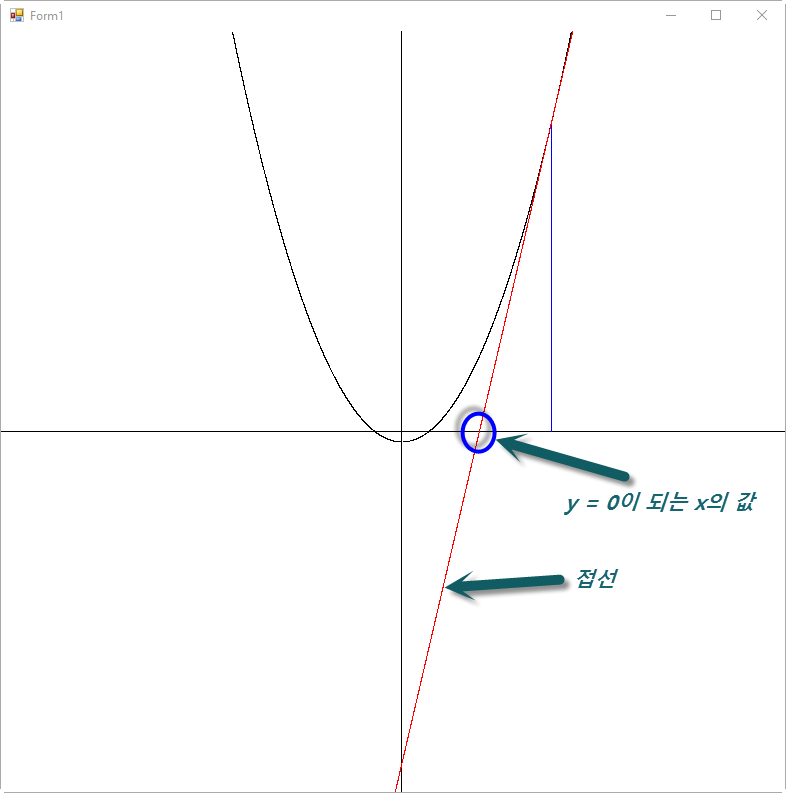
이 x 값을 구하기 위해 slopeLineFunc 접선의 방정식을 역함수로 바꾸면 되는데,
Func<float, float> slopeLineFunc = (x) => (lineSlope * x + slopeBParam);
Func<float> inverseSlopeLineFunc = (y) => ((y - slopeBParam) / lineSlope);
어차피 y 좌표의 값이 0인 순간에 대한 x 값을 구하는 것이기 때문에 다음과 같이 간략화할 수 있습니다.
Func<float> inverseSlopeLineFunc = () => (-slopeBParam / lineSlope);
float newX = inverseSlopeLineFunc();
자... 그런데, 재미있게도 새롭게 구한 newX를 가장 처음에 잡았던 임의의 x 값(150.0f) 대신 사용해 다시 수직선을 긋고 그것의 접선을 다시 구한 다음 또 newX 값을 구할 수 있게 됩니다. 프로그램도 간단합니다. 단지 위의 코드를 2번만 반복해 주면 됩니다.
float startX = 150.0f;
for (int i = 0; i < 2; i++) // 2번 반복
{
DrawVerticalLine(orgFunc, g, startX);
float lineSlope = (1 / _slopeForGraph) * 2.0f * startX;
float slopeBParam = (orgFunc(startX) - (lineSlope * startX));
Func<float, float> slopeLineFunc = (x) => (lineSlope * x + slopeBParam);
DrawTangentLine(slopeLineFunc, g);
Func<float> inverseSlopeLineFunc = () => (-slopeBParam / lineSlope);
float newX = inverseSlopeLineFunc();
startX = newX; // 마지막 x 값을 다시 피드백받아 진행
}
그래프 모양은 이렇습니다.
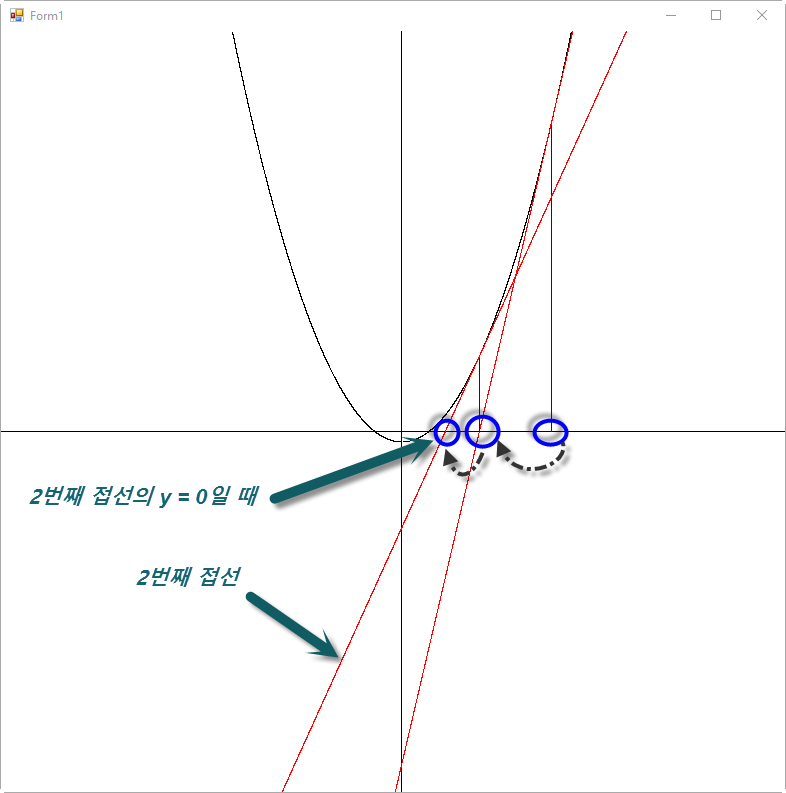
for 문의 반복을 늘려보면 자연스럽게 y = 0인 지점의 접선으로 결과가 수렴하는 것을 볼 수 있습니다.
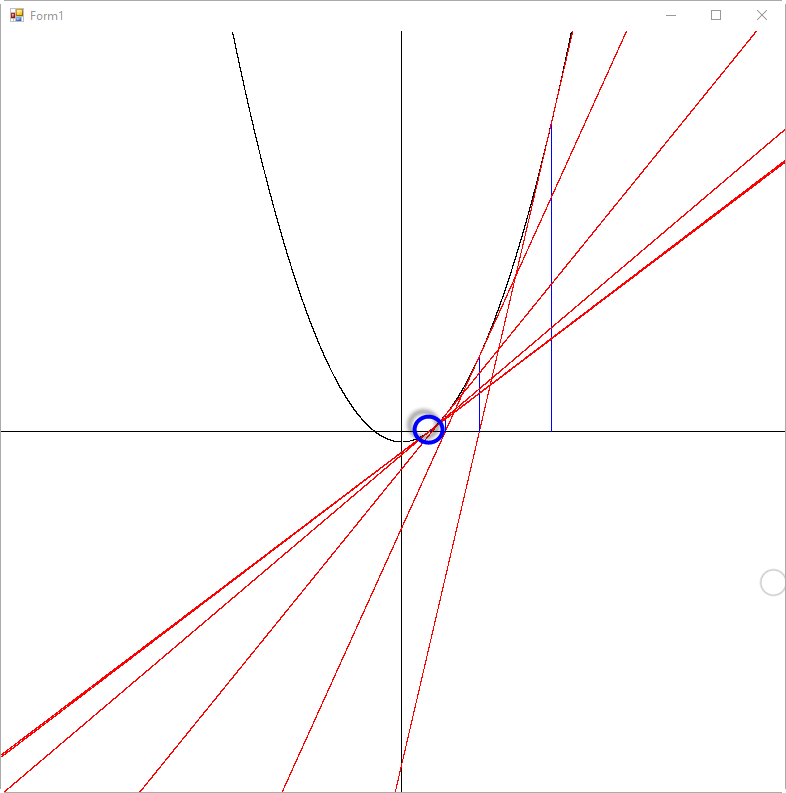
이런 성격을 가진 뉴턴-랩슨법이 제곱근을 구하는 데 사용하는 것도 역시 직관적입니다. 예를 들어 2의 제곱근의 값이 x라고 할 때 이는 x를 제곱해서 2가 나온다는 것입니다. 따라서 다음의 방정식의 해를 구하는 것과 같고,
y = x2 - 2
0 = x2 - 2 // (이때의 x 값은 2의 제곱근!)
y = 0일 때이니, 바로 위에서 "for 문의 반복을 늘려보면 자연스럽게 y = 0인 지점의 접선으로 결과가 수렴하는 것을 볼 수 있습니다." 라고 말한 내용이 결국 제곱근과 연관되어 있음을 알 수 있습니다.
간단하지요? ^^
그래서 결국 위에서 그래프를 그리기 위해 사용한 공식을 (멋진 그래프를 위해 보정한 수치를 빼면) 그대로 사용할 수 있습니다. 이를 이용해 원하는 수의 제곱근을 구하기 위한 일반적인 함수를 다음과 같이 만들 수 있습니다.
static double newtonRaphson3(double xsquare, double x0, int depth = 1)
{
Func<double, double> orgFunc = (x) => (double)(x * x - xsquare);
for (int i = 0; i < depth; i++)
{
double lineSlope = 2.0f * x0;
double slopeBParam = (orgFunc(x0) - (lineSlope * x0));
Func<double> inverseSlopeLineFunc = () => (-slopeBParam / lineSlope);
double newX = inverseSlopeLineFunc();
x0 = newX; // 마지막 x 값을 다시 피드백받아 진행
}
return x0;
}
위의 코드를 이용해 닷넷에서 기본제공되는 Math.Sqrt와 값을 비교해 테스트할 수 있습니다.
double x = 10; // 10의 제곱근을 구한다.
double x0 = x / 2; // 초기값은 5로.
Console.WriteLine(string.Format("{0}", newtonRaphson3(x, x0, 25)));
Console.WriteLine(string.Format("{0}", Math.Sqrt(x)));
x = 2; // 2의 제곱근을 구한다.
x0 = x / 2; // 초기값은 1로.
Console.WriteLine(string.Format("{0}", newtonRaphson3(x, x0, 25)));
Console.WriteLine(string.Format("{0}", Math.Sqrt(x)));
// 출력 결과
3.16227766016838
3.16227766016838
1.41421356237309
1.4142135623731
마지막으로, newtonRaphson3 메서드의 내부 코드를 좀 더 치환해서 정리하면 다음과 같이 간단한 함수 하나로 남습니다.
static double newtonRaphson4(double xsquare, double x0, int depth = 1)
{
for (int i = 0; i < depth; i++)
{
x0 = (x0 * x0 + xsquare) / (2.0f * x0);
}
return x0;
}
오~~~ 어디서 많이 보던 공식 아닌가요? ^^
뉴턴-랩슨 법(Newton-Raphson method)
; http://tro.kr/34
끝맺기 전에, 최근에 본 글에서 재미있는 공식을 봤습니다.
왜 함수형 프로그래밍이 중요한가
; https://drive.google.com/file/d/0B01vnjtP-BZsSXBnLXlfSW4zYU9zS2pXZFB4YXpOa0t0N293/view
위의 글에 보면 뉴튼-랩슨 제곱근 구하는 공식으로 다음을 소개하고 있습니다.
ai+1 = (ai + n / ai) / 2
그런데, 이 공식의 유추 과정이 재미있습니다. ^^ 미분 및 접선의 방정식을 구할 필요도 없이 그냥 다음과 같은 사고로 접근하고 있습니다.
간단하죠? ^^ 이렇게 제곱근을 구하는 방식을 "바빌로니아 법"이라 한다고! ^^
바빌로니아 법
; https://ko.wikipedia.org/wiki/%EB%B0%94%EB%B9%8C%EB%A1%9C%EB%8B%88%EC%95%84_%EB%B2%95
위의 공식에 초기값인 a를 분모/분자에 곱해주면 그것이 바로 뉴턴-랩슨법의 공식과 바로 일치합니다.
끝!
(
첨부 파일은 위의 그래프를 그리는 C# 윈폼 프로젝트와 newtonRaphson4 메서드를 테스트하는 콘솔 프로젝트를 포함합니다.)
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]