GeoGebra 기하 (18) - 원의 중심 및 접선
지오지브라 수학 앱을 이용해,
GeoGebra 기하 - 컴퍼스와 자를 이용한 작도 프로그램
; https://www.sysnet.pe.kr/2/0/11568
이번엔 원의 중심을 결정하고 접선도 그어 보겠습니다. 우선, 중심의 경우 지난 글에서 이미 답이 나왔습니다.
GeoGebra 기하 (8) - 호(Arc)의 이등분
; https://www.sysnet.pe.kr/2/0/11578
즉 아무 원호나 2개 그어,
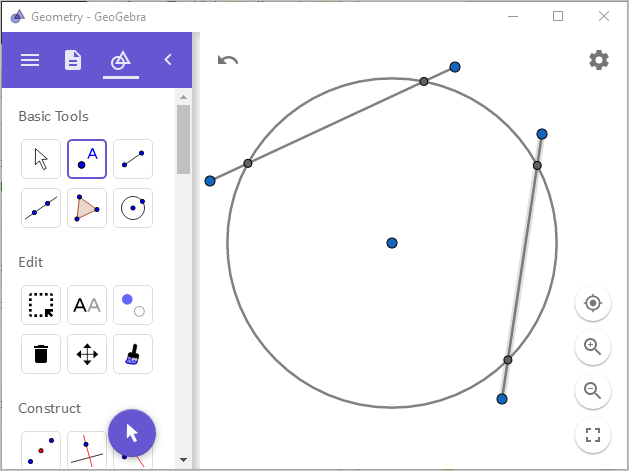
그것의 수직 이등분선(
Perpendicular Bisector)이 만나는 점이 원의 중심입니다.
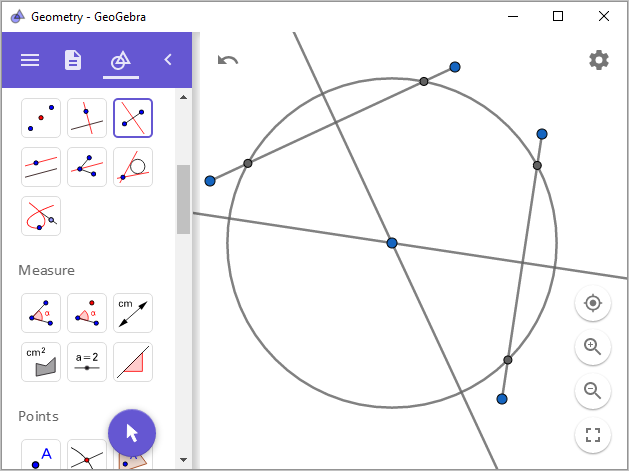
자, 그렇게 해서 점의 중심을 정했으면 이제 원 위에 있는 임의의 점에 대한 접선을 구하는 것이 가능합니다. 접선은,
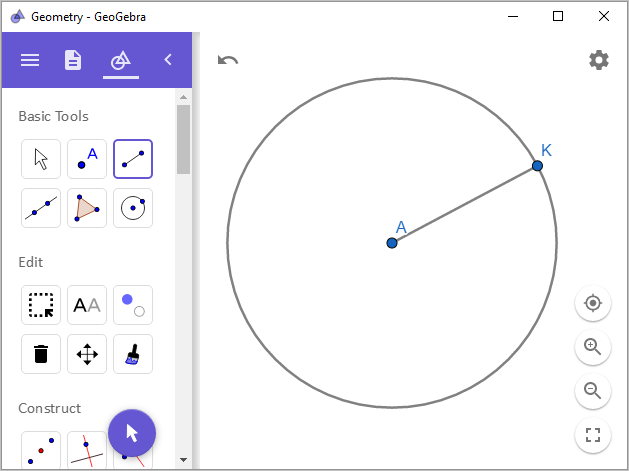
점 K와 원의 중심 A를 이은 선과 수직이기 때문에 선분 AK에 대해 점 K에서
Perpendicular Line을 이용해 수직선을 그어주면 됩니다.
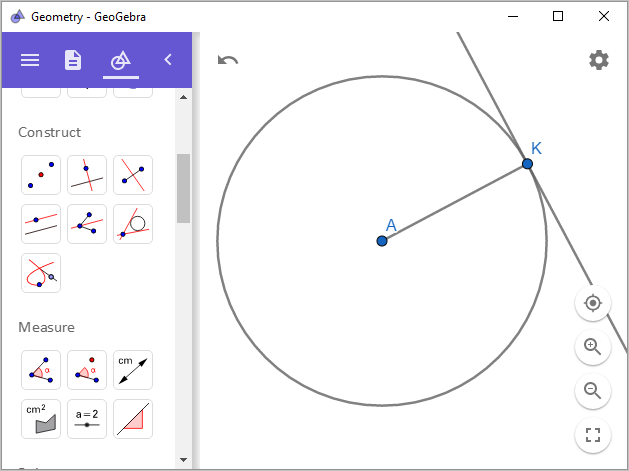
여기서 약간의 방정식을 정리해 보면, 점 A가 (0,0) 좌표에 있고 반지름이 3인 원의 방정식은 다음과 같습니다.
(x - x0)2 + (y - y0)2 = d2 (d == 반지름)
x0 = 0
y0 = 0
d = 3
x2 + y2 = 32
일반화 시켜 점 (x1, y1)이라고 하면,
x12 + y12 = d2
그리고 직선 AK의 방정식은 점 K(x
1, y
1)를 지나므로,
y = (y1 / x1) * x
이때의 접선의 기울기는 다음과 같이 구할 수 있습니다.
m = 직선 AK의 기울기
m = (y1 / x1)
m' = 점 K에서의 접선의 기울기
m * m' = -1 (수직이므로 기울기를 곱한 경우 -1)
m' = -(x1 / y1)
따라서 해당 기울기를 가진 접선의 방정식은,
y = -(x1 / y1)(x - x1) + y1
와 같습니다. 실제로 "Steps"에 나온 점 K의 위치를 이용해 직선의 방정식을 구해 볼까요? ^^
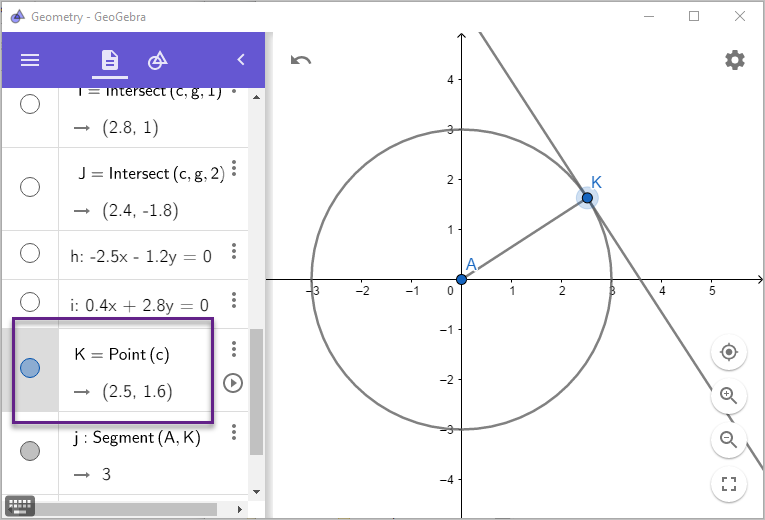
위와 같이 "Steps"를 통해서 보면 점 K의 위치가 (2.5, 1.6)임을 알 수 있습니다. 따라서 이것을 방정식에 대입해 보면,
x1 = 2.5
y1 = 1.6
y = -(2.5 / 1.6)(x - 2.5) + 1.6
= -1.5625(x - 2.5) + 1.6
= -1.5625x + 3.90625 + 1.6
= -1.5625x + 5.50625
와 같이 구할 수 있고, 이것을 역시 "Steps"에 나온 접선의 방정식과 비교해 보면,
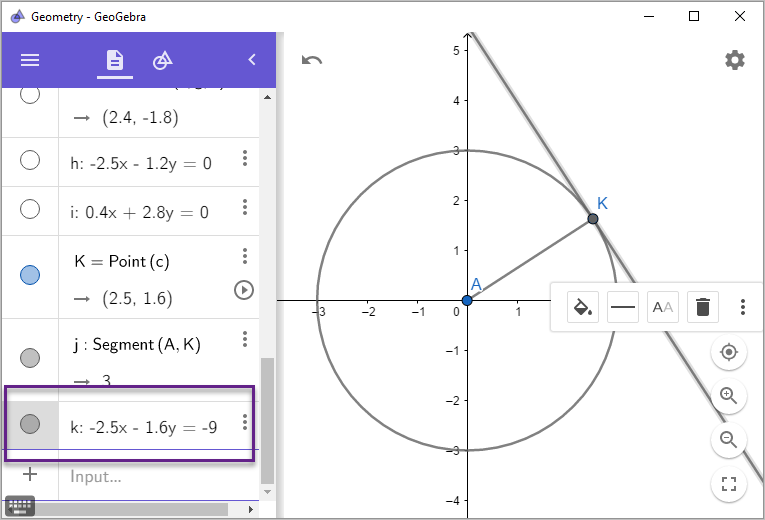
-9 = -2.5x - 1.6y
9 = 2.5x + 1.6y
1.6y = -2.5x + 9
y = -(2.5 / 1.6)x + (9 / 1.6)
= -1.5625x + 5.625
와 같이 나옵니다. y 절편에서 0.11875 정도의 오차가 있는데요, 이것은 지오지브라가 보여준 K의 좌표 (2.5, 1.6)에 소수점 2자리 이하의 값을 보여주지 않기 때문에 정확한 좌표 값에 의한 것이 아니므로 발생합니다.
참고로, 지오지브라에서 보여준 접선의 방정식은 이렇게도 구할 수 있습니다.
y = -(x1 / y1)(x - x1) + y1 (접선의 방정식)
yy1 = -(x1)(x - x1) + y12 (양변에 y1을 곱)
= -x1x + x12 + y12
x1x + yy1 = x12 + y12
x1x + y1y = d2
점 K == (2.5, 1.6)이므로,
2.5x + 1.6y = 32
그러니까, 원점 (0,0)을 기준으로 한 원이 있을 때, 점의 좌표만 알면 그것의 x
1, y
1값과 반지름을 그대로 "x
1x + y
1y = d
2" 공식에 넣고 y에 대해서 정리해 주면 접선의 방정식이 구해지는 것입니다.
마지막으로, 원 위에 있는 점이 아닌, 원 바깥에 있는 점을 지나는 접선을 작도해 보겠습니다.
간단하게, 원의 중심 A와 점 C를 잇는 선분의 이등분(
Midpoint or Center) 위치에서 원을 그려 생기는 2개의 교점을 선(
Line)으로 연결하면 됩니다.
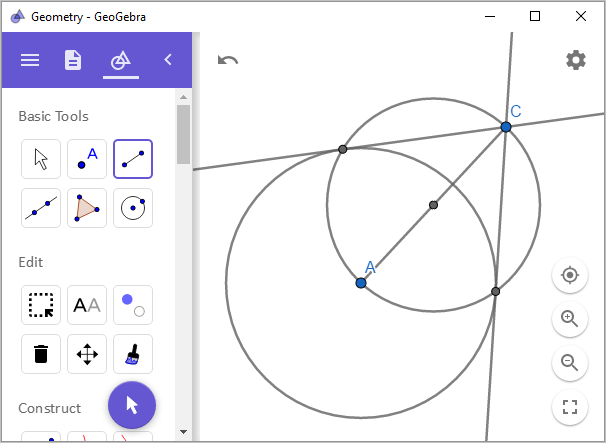
왜 그런지는 원주각 정리를 떠올리면 됩니다.
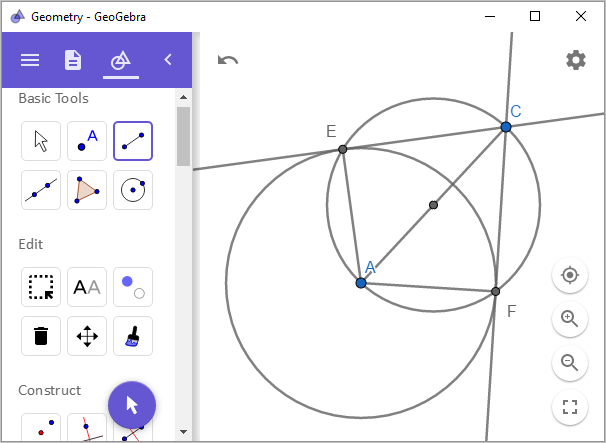
선분 AC를 지름으로 한 원이므로 중심각은 180도이고, 2개의 교점(E, F)과 이룬 각 CEA와 각 CFA는 원주각이므로 1/2이 되어 90도가 됩니다. 따라서, 점 A를 중심으로 한 원의 입장에서 보면 해당 교점들과 연결한 선은 90도를 이루므로 접선이 되는 것입니다.
(
첨부 파일은 이 글의 작도를 담은 파일입니다.)
Basic Tools
Move
Point
Segment
Line
Polygon
Circle with Center through Point
Edit
Show / Hide Label
Show / Hide Object
Construct
Midpoint or Center
Perpendicular Line
Perpendicular Bisector
Parallel Line
Angle Bisector
Measure
Angle
Angle with Given Size
Distance or Length
Lines
Segment
Segment with Given Length
Line
Ray
Circles
Circle with Center through Point
Compass
Circumcircular Arc
Polygons
Polygon
Regular Polygon
GeoGebra 메뉴 관련 기능
Steps - https://www.sysnet.pe.kr/2/0/11568
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]