C# - 그래프 그리기로 알아보는 경사 하강법의 최소/최대 값 구하기
예전에 미분을 이용한,
그래프 그리기로 알아보는 뉴턴-랩슨(Newton-Raphson's method)법과 제곱근 구하기 - C#
; https://www.sysnet.pe.kr/2/0/10911
방정식의 근사해를 알아본 적이 있는데요. 도함수의 다음과 같은 특성을 이용하면,
f' < 0: 최솟값은 우측에.
f' = 0: 최솟값
f' > 0: 최솟값은 좌측에.
최솟값을 (그 반대로는 최댓값을) 근사할 수 있습니다. 예를 들어, f(x) = x^2 - 2x + 1이라는 방정식이 있다면,
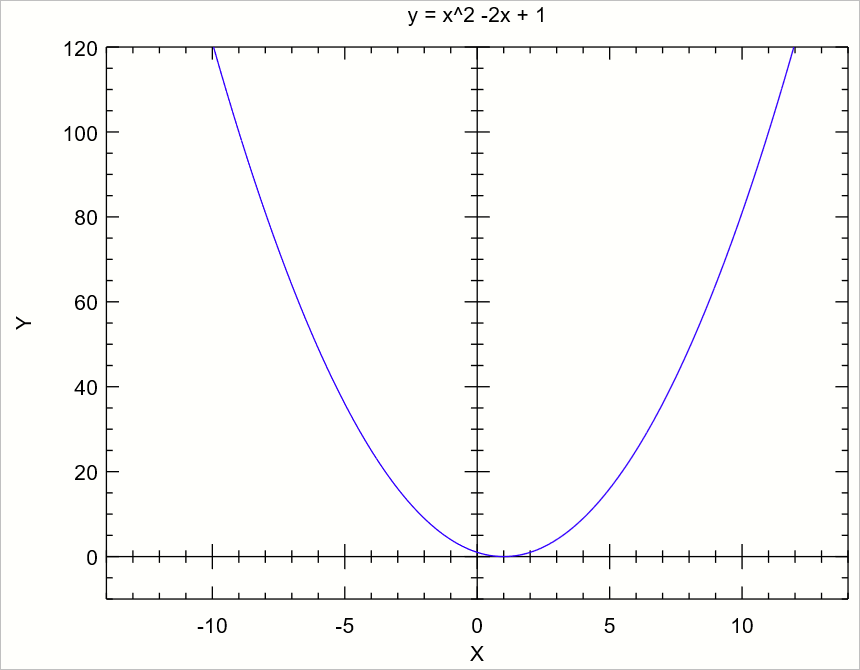
이것의 도함수는 f'(x) = 2x - 2가 되고, (무작위로 선정한) x = 10으로 시작하는 경우 최솟값을 다음과 같이 이동하면서 근사할 수 있습니다.
f'(10) = 18 > 0: 최솟값은 좌측에 있으므로 다음번 x는 좀 더 작게 시도.
f'( 9) = 16 > 0: "
f'( 8) = 14 > 0: "
... : "
f'( 1) = 0 = 0: 최솟값
물론 위의 경우에는 1씩 줄여나가다 운이 좋아 정확히 최솟값 위치에 왔지만 단순하지 않은 상황에서는 근삿값에 대한 범위를 마련하고 그것을 만족하는 수준이거나, 아니면 근삿값으로 진행하는 과정 중에 원하는 수준만큼의 변화가 없다면 중단하는 식으로 작성하면 됩니다.
코드로 만들어 보면,
using MathNet.Numerics.Random;
using PLplot;
using System;
using System.Linq;
namespace ConsoleApp2
{
class Program
{
static void Main(string[] args)
{
Func<double, double> f = (x) => (x - 1) * (x - 1);
Func<double, double> df = (x) => 2 * x - 2;
// 그래프 출력
DrawPlotChart(-14, 14, -10, 120, f, df);
}
private static void DrawPlotChart(double xMin, double xMax, double yMin, double yMax,
Func<double, double> orgDrawFunc, Func<double, double> dfDrawFunc)
{
string chartFileName = "click.svg";
using (var pl = new PLStream())
{
pl.sdev("svg");
pl.sfnam(chartFileName);
pl.spal0("cmap0_alternate.pal");
pl.init();
pl.env(xMin, xMax, yMin, yMax, AxesScale.Independent, AxisBox.BoxTicksLabelsAxes);
pl.lab("X", "Y", "y = x^2 - 2x + 1");
pl.spal0("");
pl.col0(PLplot.Color.Blue);
// y = x ^ 2 - 2x + 1 그래프를 그리고,
{
double[] ptX = Utils.RangeInclusive(xMin, xMax, 0.01).ToArray();
double[] ptY = null;
ptY = new double[ptX.Length];
for (int i = 0; i < ptX.Length; i++)
{
ptY[i] = orgDrawFunc(ptX[i]);
}
pl.line(ptX, ptY);
}
char code = Symbol.Bullet;
pl.col0(PLplot.Color.Blue);
// x = 15에서 시작해 도함수의 결과에 따라 0.1씩 변위를 주며 최솟값으로 이동하는 과정을 점으로 출력
int maxTrial = 1000;
double anyX = 15.0; // 랜덤 값
while (maxTrial-- > 0)
{
double yPos = dfDrawFunc(anyX);
pl.Point(anyX, orgDrawFunc(anyX), code);
if (yPos.GetCloseToZeroSlope())
{
break;
}
else anyX += (yPos > 0) ? -0.1 : 0.1;
}
pl.eop();
pl.gver(out var verText);
}
}
}
public static class Utils
{
public static IEnumerable<T> RangeInclusive<T>(T start, T stop, T step)
{
dynamic dStart = start;
dynamic dStop = stop;
dynamic dStep = step;
if (dStep == 0)
throw new ArgumentException("Parameter step cannot equal zero.");
if (dStart < dStop && dStep > 0)
{
for (var i = dStart; i <= dStop; i += dStep)
{
yield return i;
}
}
else if (dStart > dStop && dStep < 0)
{
for (var i = dStart; i >= dStop; i += dStep)
{
yield return i;
}
}
}
public static void Point(this PLStream pl, double x, double y, char code)
{
pl.poin(new double[] { x }, new double[] { y }, code);
}
public static bool GetCloseToZeroSlope(this double value)
{
return Math.Abs(value) < 1e-03 ? true : false;
}
}
}
다음과 같은 출력을 얻을 수 있습니다.
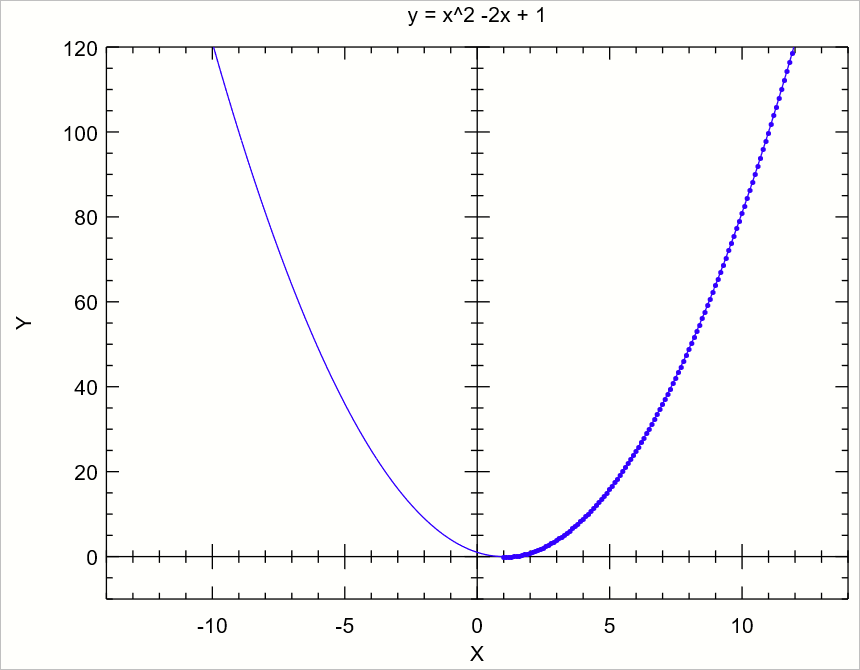
보는 바와 같이 최솟값으로 잘 수렴하고 있죠! ^^
"
그래프 그리기로 알아보는 뉴턴-랩슨(Newton-Raphson's method)법과 제곱근 구하기 - C#" 글을 보면, 도함수로 접근하면서 처음에는 크게 이동하다가 점차 간격이 작아지게 되는데 마찬가지로 경사 하강법도 단순하게 x의 값을 일정 수로 줄여나가기 보다 다음과 같은 식으로 이전 x 값 기준으로 줄여나가는 방식이 있습니다.
x := x - f'(x)
하지만, 단순히 위와 같이 하면 f'(x)의 반환값이 크기 때문에 x 값의 부호를 반대로 만들어 근삿값을 진동하는 식으로 접근하게 됩니다. 이런 문제를 해결하기 위해 약간의 조정값을 f'(x)에 곱해주면,
x := x - n * f'(x) // n == 학습 비율(learning rate)
// 예를 들어 n = 0.1
즉, 이전 코드를 다음과 같이 개선한 후,
anyX = 15.0;
double t = 0.1;
while (maxTrial-- > 0)
{
double yPos = dfDrawFunc(anyX);
pl.Point(anyX, orgDrawFunc(anyX), code);
if (yPos.GetCloseToZeroSlope())
{
break;
}
else anyX -= (t * yPos);
}
결과를 보면, 훨씬 빨리 최솟값으로 수렴하는 것을 확인할 수 있습니다.
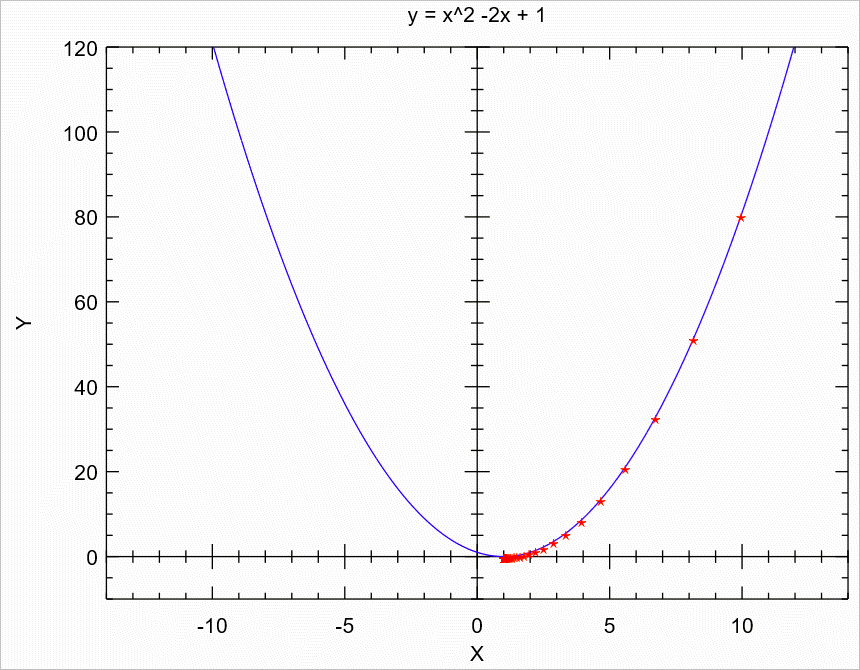
(
첨부 파일은 이 글의 예제 코드를 포함합니다.)
수렴을 좀 더 빨리하기 위해, 데이터에 대한 전처리를 수행하는 과정이 바로 정규화입니다. 예를 들어 이전 글을 보면,
ML.NET 데이터 정규화
; https://www.sysnet.pe.kr/2/0/11922
click.csv 파일의 x 값 범위가 25 ~ 272에 해당하는데 이것을 z-score 정규화를 거치면 -1.7406785589738 ~ 1.94669368859505가 되어 수렴을 시작할 수 있는 랜덤 값 범위를 대폭 줄이게 됩니다.
참고로, 직관적으로 아시겠지만 ^^ 경사 하강법은,
경사 하강법
; https://ko.wikipedia.org/wiki/%EA%B2%BD%EC%82%AC_%ED%95%98%EA%B0%95%EB%B2%95
지역 근사해는 찾아도, 전역 근사해를 찾지 못할 수 있습니다. 아래의 그래프와 같은 상황들을 보면 이해가 되실 것입니다. ^^
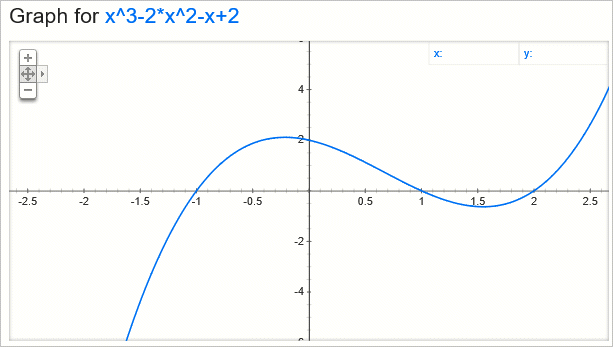
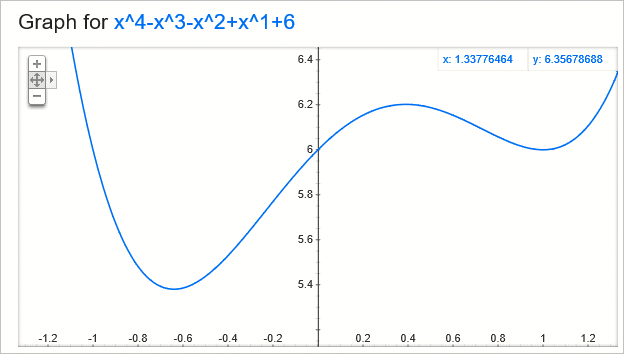
이에 대한 보완으로 "확률 경사 하강법"과 "미니 배치법"이 있다고 하니 좀 더 자세한 사항은 "
기초 수학으로 이해하는 머신러닝 알고리즘" 책을 보시면 되겠습니다. ^^
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]