GeoGebra 기하 (23) - sqrt(n) 제곱근
지오지브라 수학 앱을 이용해,
GeoGebra 기하 - 컴퍼스와 자를 이용한 작도 프로그램
; https://www.sysnet.pe.kr/2/0/11568
이번에는 제곱근에 대한 작도를 해보겠습니다. 우선 가장 쉬운 ${ \sqrt {2} }$로 시작해 볼까요? ^^ 방정식으로 보면,
x2 - 2 = 0
x2 = 2
x = ${ \sqrt {2} }$
가 되고, 단위 길이를
Segment with Given Length를 이용해 작도하고, 그 단위 선분의 끝 점에서 수직인 직선을 그은(
Perpendicular Line) 결과 제곱근 2를 구하게 됩니다.
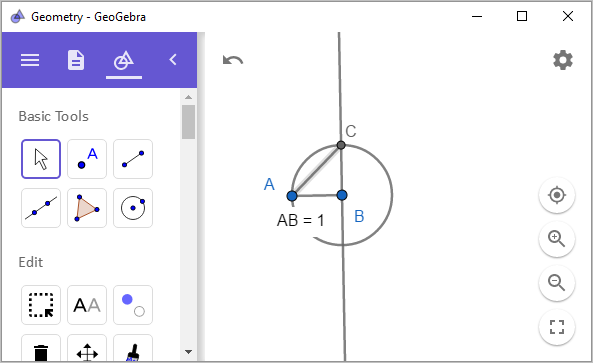
즉, 선분 AC의 길이가 ${ \sqrt {2} }$에 해당합니다. 피타고라스 정리를 생각해 보면 간단하게 증명이 됩니다.
AC2 = AB2 + AC2
AB = AC = 1이므로,
AC2 = 2
AC = ${ \sqrt {2} }$
제곱근 2를 작도했다는 것과 함께 지난 글의 4칙 연산을 추가하면,
GeoGebra 기하 (6) - 대수의 4칙 연산
; https://www.sysnet.pe.kr/2/0/11576
다음의 수에 해당하는 것들은 모두 작도할 수 있다는 것이 됩니다.
a + b${ \sqrt {2} }$ (a, b는 유리수)
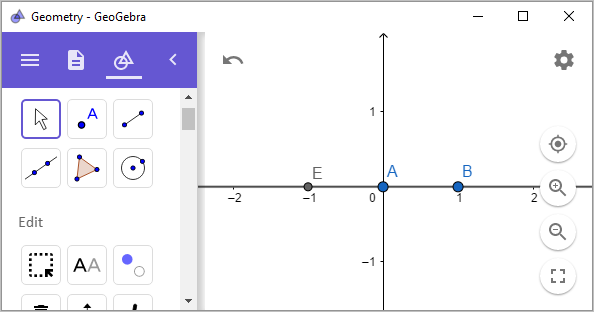
그렇다면 ${ \sqrt {3} }$은 어떻게 작도할까요? 단위 길이를
한 직선에 다음과 같이 2개를 작도하고,
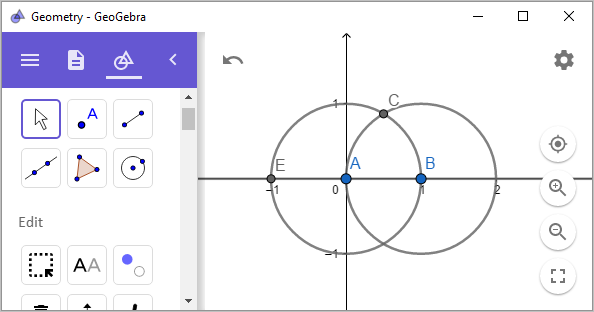
선분 AB를 반지름으로 하는 원을 점 A와 점 B를 중심으로 원을 2개 그리면 그 교점이 생깁니다.
점 C로부터 점 E와 점 B에 선분을 그으면 삼각형 EBC가 작도되는데요,
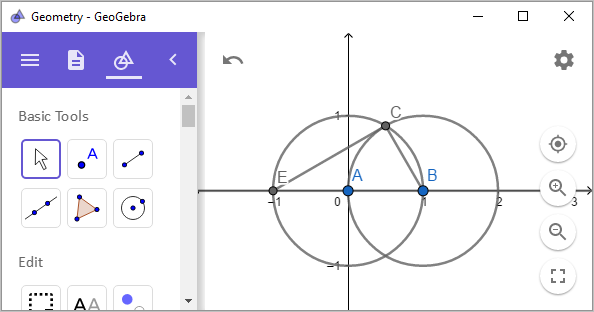
이번에도 역시 피타고라스 정리에 의해 따라서 다음과 같은 식이 성립하고,
EB2 = EC2 + CB2
EB = 2, CB = 1이므로,
4 = EC2 + 1
3 = EC2
${ \sqrt {3} }$= EC
선분 EC로 제곱근 3을 작도했으니, 이번에도 역시 다음의 수들은 모두 작도할 수 있게 됩니다.
a + b${ \sqrt {3} }$ (a, b는 유리수)
혹시, 다음과 같이 임의의 길이 a를 가진 경우에도 제곱근이 가능할까요? 즉, 유리수 a에 대한 제곱근이 가능하냐는 것입니다.
이를 위해, 선분 AB를 늘려 단위 길이 1만큼 더 작도(
Segment with Given Length)합니다.
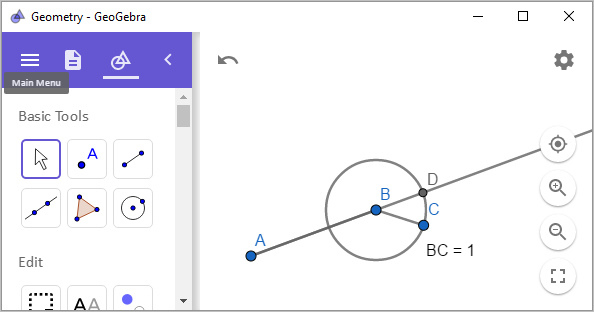
연장된 선분 AD를 이등분(
Midpoint or Center)하고, 그 중점을 중심으로 한 원을 그려줍니다.
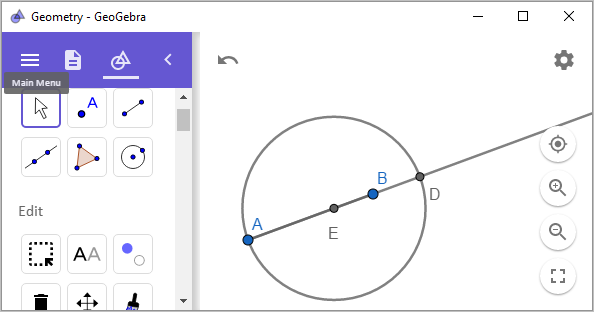
마지막으로, 점 B에서 수직선을 그리고(
Perpendicular Line), 그 수직선과 원 E와 만나는 교점을 점 A와 점 D에 각각 선분을 연결해 줍니다.
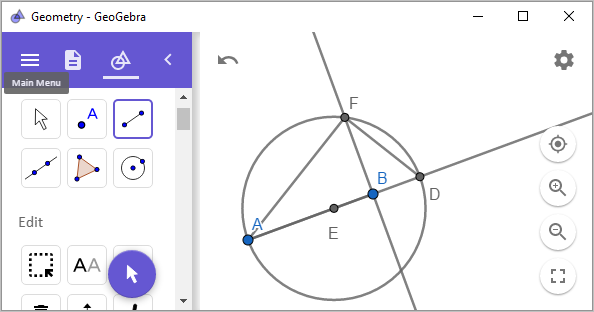
이때 선분 FB가 이루는 선이 바로 제곱근 a의 길이가 됩니다. 증명을 해볼까요? ^^ 중심각/원주각에 의해 각 AFD는 직각이고, 각 FBD도 수직선을 그었으므로 직각이 됩니다. 또한 삼각형 내각의 합이 180도이므로,
삼각형 AFD
각 AFD + 각 FAD + 각 FDA = 180
90 + 각 FAD + 각 FDA = 180
삼각형 FBD
각 DFB + 각 FBD + 각 BDF = 180
각 DFB + 90 + 각 BDF = 180
위의 각에서 각 FDB를 각 FDA와 각 BDF로 공유하고 있으므로 이를 x로 두었을 때,
삼각형 AFD
90 + 각 FAD + x = 180
삼각형 FBD
각 DFB + 90 + x = 180
결국 각 FAD와 각 DFB가 같게 됩니다. 그럼 이제 삼각형 AFB와 삼각형 FBD를 보겠습니다. 결국 2개의 각이 같으므로 닮음 조건이 성립하고, 이에 기반해 다음의 비율을 정리할 수 있습니다.
선분 BA : 선분 FB = 선분 FB : 선분 BD
==> 선분 FB * 선분 FB = 선분 BA * 선분 BD
==> (선분 FB)2 = 선분 BA * 선분 BD
선분 BD는 단위 길이 1이므로,
==> (선분 FB)2 = 선분 BA
선분 BA의 길이는 우리가 설정했던 유리수 a의 길이,
==> (선분 FB)2 = a
==> (선분 FB) = ${ \sqrt {a} }$
이로써, 제곱근과 관련한 아래의 모든 수를 작도할 수 있게 되었습니다.
a + b${ \sqrt {n} }$ (a, b는 유리수)
(
첨부 파일은 이 글의 작도를 담은 파일입니다.)
Basic Tools
Move
Point
Segment
Line
Polygon
Circle with Center through Point
Edit
Show / Hide Label
Show / Hide Object
Construct
Midpoint or Center
Perpendicular Line
Perpendicular Bisector
Parallel Line
Angle Bisector
Measure
Angle
Angle with Given Size
Distance or Length
Lines
Segment
Segment with Given Length
Line
Ray
Circles
Circle with Center through Point
Compass
Circumcircular Arc
Polygons
Polygon
Regular Polygon
GeoGebra 메뉴 관련 기능
Steps - https://www.sysnet.pe.kr/2/0/11568
Animation
Settings - https://www.sysnet.pe.kr/2/0/11602
Show Trace
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]