C# - 다항식을 위한 최소 자승법(Least Squares Method)
지난 글에서,
C# - 행렬식을 이용한 최소 자승법(LSM: Least Square Method)
; https://www.sysnet.pe.kr/2/0/11918
최소 자승법(최소 제곱법)을 이용해 1차 함수로 근사하는 것을 봤는데요, 이를 2차, 3차,...로 확장하는 것은 다음과 같이 매우 쉽습니다.
다항식(Polynomial): aXn 형식의 항들의 합으로 구성된 식
a: 계수(Coefficient)
X: 변수(Variable)
n: 지수(Exponent)
θ0 + θ1x1 + θ2x12 = y1
θ0 + θ1x2 + θ2x22 = y2
...
θ0 + θ1xn + θ2xn2 = yn
θ0 + θ1x1 + θ2x12 + θ3x13 = y1
θ0 + θ1x2 + θ2x22 + θ3x13 = y2
...
θ0 + θ1xn + θ2xn2 + θ3x13 = yn
따라서 행렬을 사용하는 경우 그냥 늘어나는 방정식의 계수만큼 행을 추가해 의사역행렬을 구한 후 연산하면 매개변수를 구할 수 있습니다.
private static double[] GetPolynomial(double[] xData, double[] yData, int numberOfEfficient)
{
Matrix<double> matA = CreateMatrix.DenseOfColumnMajor(xData.Count(), 1, xData);
Vector<double> add1 = Vector<double>.Build.DenseOfArray(Enumerable.Repeat(1.0, xData.Count()).ToArray());
matA = matA.InsertColumn(1, add1);
for (int i = 1; i < numberOfEfficient; i++)
{
double[] newColumnData = xData.Select((elem) => Math.Pow(elem, i + 1)).ToArray();
Vector<double> addX = Vector<double>.Build.DenseOfArray(newColumnData);
matA = matA.InsertColumn(0, addX);
}
Console.WriteLine(matA);
Matrix<double> matB = CreateMatrix.DenseOfColumnMajor(yData.Count(), 1, yData);
Matrix<double> pinvMatA = matA.PseudoInverse();
Console.WriteLine(pinvMatA);
Matrix<double> matX = pinvMatA * matB;
return matX.AsColumnMajorArray();
}
[파란색 - 1차 함수, 빨간색 - 2차 함수, 노란색 3차 함수]
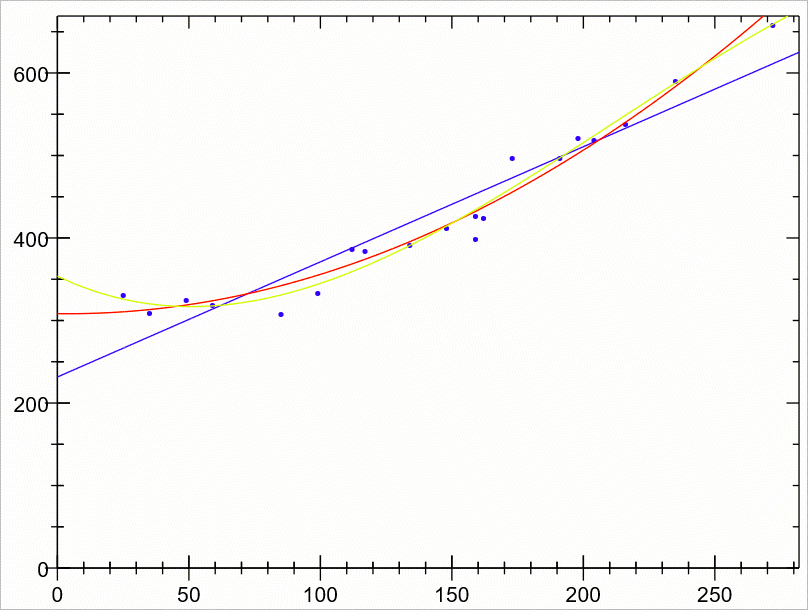
일반적으로 차수가 올라갈수록 (과적합의 문제가 발생할 수 있지만) 오류는 더 적어집니다. 확인을 위해 간단하게 다음과 같이 작성해 보면,
private static void ReportError(double[] xData, double[] yData, Func<double, double> func)
{
double error = 0.0;
for (int i = 0; i < xData.Length; i ++)
{
double diff = yData[i] - func(xData[i]);
error += (diff * diff);
}
Console.WriteLine("Error: " + error);
}
/*
1차: Error: 19086.9489618992
2차: Error: 6555.72459287144
3차: Error: 5038.32058563331
*/
1차에 비해 2차에서 두드러지게 오류가 낮아지는 것을 볼 수 있습니다. 따라서 이런 경우 효율을 고려한다면 2차 함수를 사용하는 것이 좋은 선택일 수 있습니다.
(
첨부 파일은 이 글의 예제 코드를 포함합니다.)
지난 글에서 행렬 라이브러리를 직접 사용하지 않고 1차 근사식에 대한 매개 변수를 구하는 방법을 알아봤는데요,
C# - 최소 자승법의 1차 함수에 대한 매개변수를 단순 for 문으로 구하는 방법
; https://www.sysnet.pe.kr/2/0/11919
말 그대로 연립 방정식이므로 가우스 소거법을 이용해 매개 변수를 구하는 것도 가능합니다. 코드가 눈에 잘 안 들어오지만 어차피 복붙으로 써야 하는 것이라 큰 문제는 안 될 것입니다. ^^
Linear Equation Solver - Gaussian Elimination (C#)
; https://www.codeproject.com/Tips/388179/Linear-Equation-Solver-Gaussian-Elimination-Csharp
Gaussian elimination
; https://rosettacode.org/wiki/Gaussian_elimination#C.23
Solve a system of equations with Gaussian elimination in C#
; http://csharphelper.com/blog/2014/10/solve-a-system-of-equations-with-gaussian-elimination-in-c/
[C#/WINFORM] 다항식 최소 제곱법(Polynomial Least Squares Method) 사용하기
; https://icodebroker.tistory.com/5580
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]