GeoGebra 기하 - 컴퍼스와 자를 이용한 작도 프로그램
지오지브라 수학 앱이란 것이 있습니다.
지오지브라 수학 앱
; https://www.geogebra.org/
이 중에서 "기하" 앱이 있는데 요게 ^^ 은근히 재미있습니다. 대수학과 관련한 책을 읽다 보면 컴퍼스와 자를 이용한 작도가 나오곤 하는데, 그럴 때 위의 링크를 방문해 "기하" 응용 프로그램을 다운로드하면 컴퓨터로 직접 실습해가며 책을 읽을 수 있습니다. ^^
처음 시작하면 "Basic Tools"만 도구 상자에 보이는데, "MORE" 버튼을 눌러 (2번까지) 확장하면 "Edit", "Construct", "Measure", "Points", "Lines", "Circles", "Polygons", "Conics", "Transform", "Media", "Others" 범주의 기능을 선택할 수 있습니다.
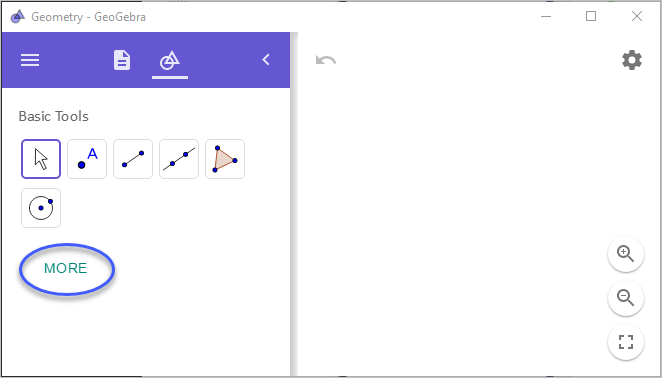
도구를 이용해 그리다 보면,
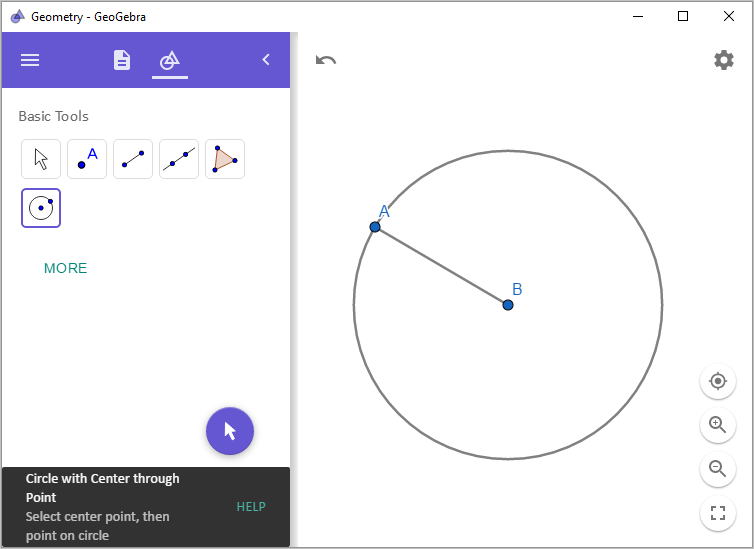
"Steps" 보기로 전환해 따라온 절차를 확인하는 것도 가능합니다.
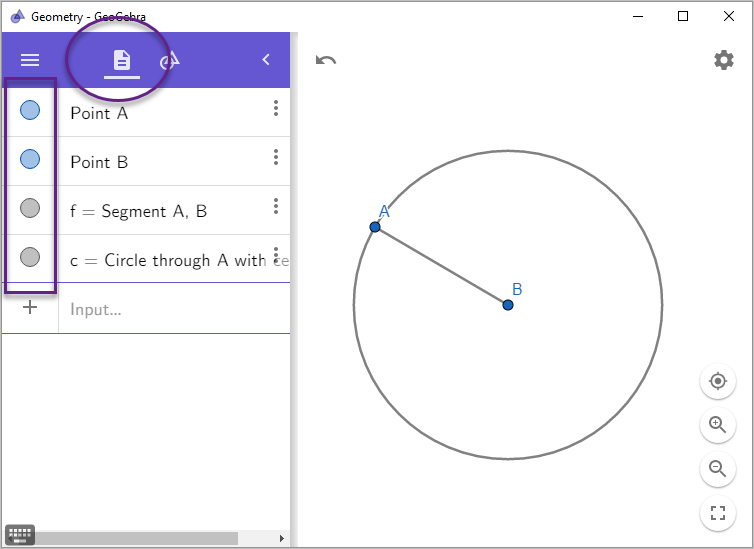
Point A
Point B
f = Segment A, B
c = Circle through A with center B
그리고, 위의 왼쪽에 있는 동그라미를 눌러 특정 기하 요소를 토글 식으로 화면에 보이거나 사라지게 선택할 수 있습니다.
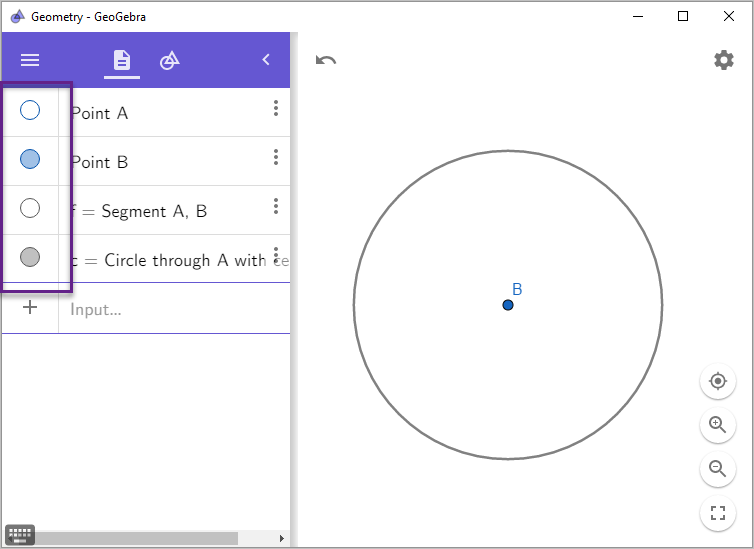
마지막으로, 수동 애니메이션(?) 기능이 있는데 요것도 좀 재미있습니다. 간단한 실습을 위해 주어진 AB 선분을 2등분 하는 선을 다음과 같이 (미리 도구로 제공하는 "Perpendicular Bisector"를 이용해) 쉽게 작도할 수 있습니다.
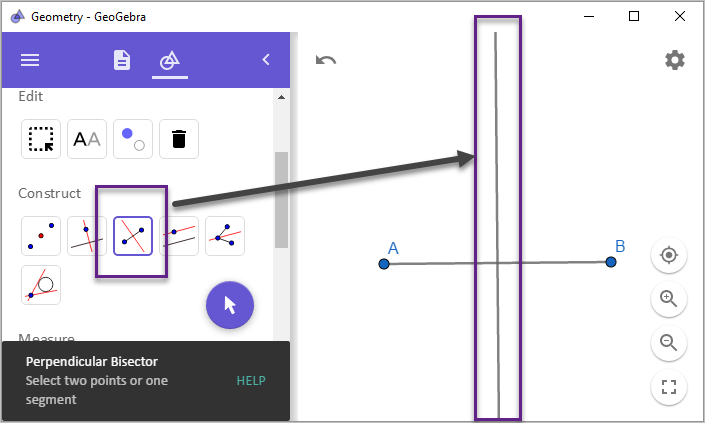
그 교점에, 잘 맞춰서 점을 하나 찍어줍니다.
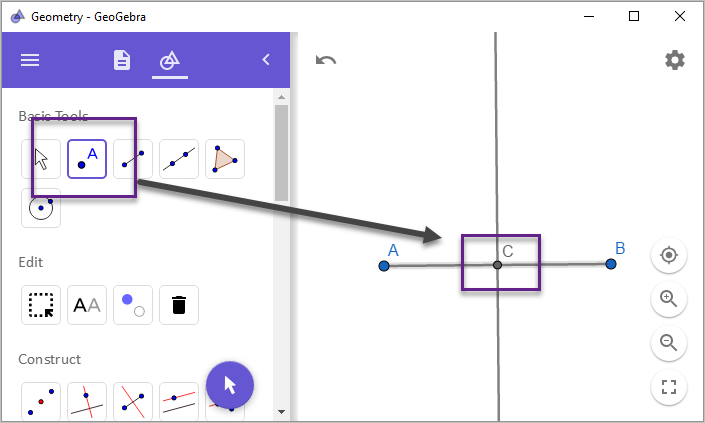
그런데, 점 C의 모양이 점 A, B와는 다소 작고 색상도 다릅니다. 이런 유의 점들은 계산에 의해 정해지는 점으로 사용자가 임의로 이동할 수 없음을 의미하기도 합니다. 실제로 마우스를 이용해 점 C를 클릭하고 누른 채로 이동시킬 수 없지만, 점 A와 점 B는 마우스를 이용해 이동이 가능합니다. 그래서 점 A와 점 B를 자유롭게 이동해도 그에 따라 이등분 선이 유지가 됩니다.
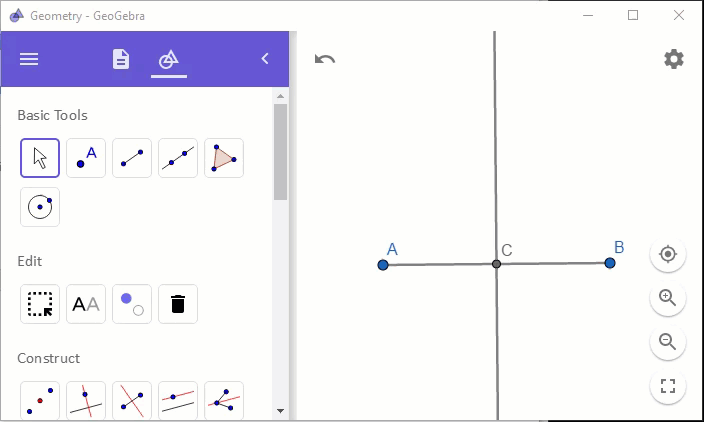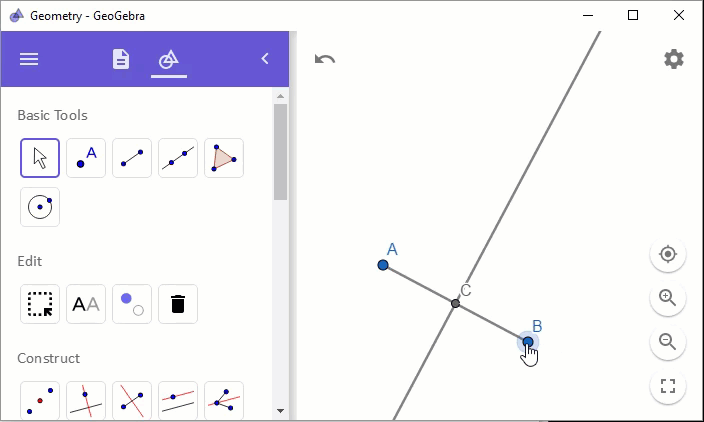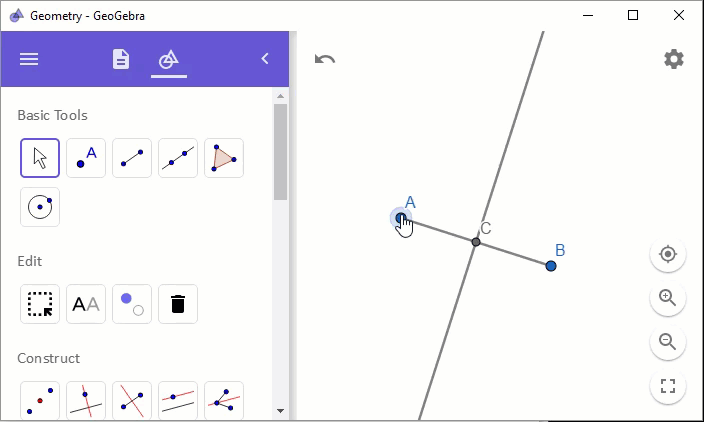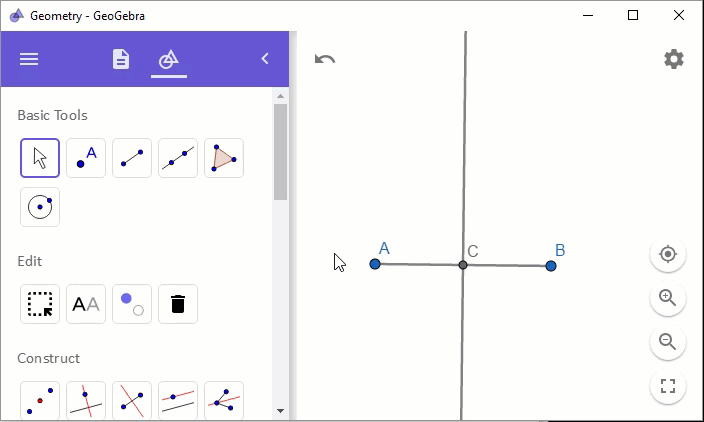
위의 기하 상태를 "Steps"로 보면 다음과 같습니다.
Point A
Point B
f = Segment A, B
g = Perpendicular Bisector of AB
C = Intersection of g and f
점 A, B는 임의로 정해진 반면, Line인 f, g는 점 A, B에 의해 결정되었고, 점 C는 Line인 g, f에 의해 결정된 것임을 알 수 있습니다. 마지막으로 이렇게 작도한 내용을 ggb 파일로 저장할 수 있는데 "이미지"로써 저장하지 않고 "Steps"를 저장하는 것이기 때문에 다른 사람이 해당 ggb 파일을 열어 "Steps"를 보면서 작도를 쉽게 재현해 볼 수 있습니다.
어떠세요? ^^ 앞으로 수학 책 보면서 나오는 기하 내용은 저렇게 컴퓨터로 작도를 직접 해보면 더 재미있지 않을까요? ^^
GeoGebra 기하 (1) - 수직 이등분선
; https://www.sysnet.pe.kr/2/0/11569
GeoGebra 기하 (2) - 임의의 선분과 특정 점을 지나는 수직선
; https://www.sysnet.pe.kr/2/0/11570
GeoGebra 기하 (3) - 평행선
; https://www.sysnet.pe.kr/2/0/11573
GeoGebra 기하 (4) - 선분을 n 배 늘이는 방법
; https://www.sysnet.pe.kr/2/0/11574
GeoGebra 기하 (5) - 선분을 n 등분하는 방법
; https://www.sysnet.pe.kr/2/0/11575
GeoGebra 기하 (6) - 대수의 4칙 연산
; https://www.sysnet.pe.kr/2/0/11576
GeoGebra 기하 (7) - 각의 이등분
; https://www.sysnet.pe.kr/2/0/11577
GeoGebra 기하 (8) - 호(Arc)의 이등분
; https://www.sysnet.pe.kr/2/0/11578
GeoGebra 기하 (9) - 임의의 선분을 한 변으로 갖는 정삼각형
; https://www.sysnet.pe.kr/2/0/11579
GeoGebra 기하 (10) - 직각의 3등분
; https://www.sysnet.pe.kr/2/0/11580
GeoGebra 기하 (11) - 3대 작도 불능 문제의 하나인 임의 각의 3등분
; https://www.sysnet.pe.kr/2/0/11581
GeoGebra 기하 (12) - 삼각형의 내심과 내접하는 원
; https://www.sysnet.pe.kr/2/0/11584
GeoGebra 기하 (13) - 삼각형의 외심과 외접하는 원
; https://www.sysnet.pe.kr/2/0/11585
GeoGebra 기하 (14) - 삼각형의 무게 중심
; https://www.sysnet.pe.kr/2/0/11586
GeoGebra 기하 (15) - 삼각형의 수심
; https://www.sysnet.pe.kr/2/0/11590
GeoGebra 기하 (16) - 삼각형의 방심과 방접원
; https://www.sysnet.pe.kr/2/0/11591
GeoGebra 기하 (17) - 각의 복사
; https://www.sysnet.pe.kr/2/0/11593
GeoGebra 기하 (18) - 원의 중심 및 접선
; https://www.sysnet.pe.kr/2/0/11594
GeoGebra 기하 (19) - 두 원의 안과 밖으로 접하는 직선
; https://www.sysnet.pe.kr/2/0/11599
GeoGebra 기하 (20) - 세 점을 지나는 원
; https://www.sysnet.pe.kr/2/0/11600
GeoGebra 기하 (21) - 반전기하학의 직선 및 원에 관한 반사변환
; https://www.sysnet.pe.kr/2/0/11601
GeoGebra 기하 (22) - 반전기하학의 원에 관한 반사변환
; https://www.sysnet.pe.kr/2/0/11602
GeoGebra 기하 (23) - sqrt(n) 제곱근
; https://www.sysnet.pe.kr/2/0/11603
GeoGebra 기하 (24) - 정다각형
; https://www.sysnet.pe.kr/2/0/11604
[이 글에 대해서 여러분들과 의견을 공유하고 싶습니다. 틀리거나 미흡한 부분 또는 의문 사항이 있으시면 언제든 댓글 남겨주십시오.]